Table of Contents
Definition
The inverse is shown by putting a little “-1” after the function name, like this:
f-1(y), where y = f(x)
It says “f inverse of y“
Here we have the function f(x) = 3x+2
The flow is
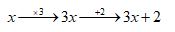
Inverse Functions make 3x + 2 back to x
![]() , substitute y = 3x + 2,
, substitute y = 3x + 2,
then
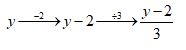
So, the inverse of f(x) = 3x + 2 is f-1(y) =
Let’s put x = 3 on f(x):
f(3) = 3×3 + 2 = 11
Then put y = 11 on f-1(y):
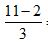
f-1(11) = = 3
So,
f-1(y)=f-1(f(x)) = x
Then, how about f (f-1(x)) ?
Because f-1(y)= x, then f (f-1(y)) = f (x) = y
f (f-1(y)) = y. Which means f (f-1(x)) = x
So
f-1(f(x)) = f (f-1(x)) = x
Inverses of Common Functions
So far is easy, because we know the inverse of Add is Subtract, and the inverse of Multiply is Divide. Ho about other functions?
List of inverse of Multiply is Divide
| Inverse | Note |
| + <=> – | |
| x <=> ÷ | Can’t divide by zero |
| 1/x <=> 1/y | x and y not zero |
| x2 <=> √y | x and y ≥ 0 |
| n not zero (different rules when n is even, odd, positive, or negative) | |
| ex <=> ln(y) | y > 0 |
| ax <=> loga(y) | y and a > 0 |
| sin(x) <=> sin-1(y) | -π/2 to +π/2 |
| cos(x) <=> cos-1(y) | 0 to π |
| tan(x) <=> tan-1(y) | -π/2 to +π/2 |
Invers Function Examples
1. Determine the invers function
- f(x) = 2x – 3
- a(x) = ½ x – 4
- f(y) = (y-2)3 – 2
- h(x) = (-x + 3) / 5
- g(x) = 2sinx + 1
- f(x) = 2x – 3
replace f(x) with y
y = 2x – 3
y + 3 = 2x
(y+3)/2 = x
Then f-1(x) = (x+3) / 2
- a(x) = ½ x – 4
replace a(x) with y
y = ½ x – 4
y + 4 = ½ x
2y + 8 = x
Then a-1(x) = 2x + 8
- f(y) = (y-2)3 – 2
replace f(y) with a
a = (y-2)3 – 2
a + 2 = (y-2)3
3√(a+2) = y – 2
3√(a+2) + 2 = y
Then f-1(y) = 3√(y+2) + 2
- h(x) = (-x + 3) / 5
replace h(x) with y
y = (-x + 3) / 5
5y = -x + 3
5y – 3 = -x
x = -5y + 3
then h-1(x) = -5x + 3
- g(x) = 2sinx + 1
replace g(x) with y
y = 2 sinx + 1
y – 1 = 2 sinx
(y – 1) / 2 = sin x
x = arc sin{(y – 1) / 2}
then g-1(x) = arc sin{(x – 1) / 2}
2. Determine the domain of invers function
- g(x) = -¼x – ¾
- k(x) = 4x / (2x-1)
- f(x) = {√(2x-1)} / 4
- b(x) = 2x¾ + 1
- g(x) = -¼x – ¾
y = -¼x – ¾
y + ¾ = -¼x
-4y – 3 = x
g-1(x) = -4x – 3
then D(g-1) = all real numbers.
- k(x) = 4x / (2x-1)
y = 4x / (2x-1)
2xy – y = 4x
2xy – 4x = y
x(2y – 4) = y
x = y / (2y – 4)
k-1(x) = x / (2x – 4)
then D(k-1) = all real numbers except 2.
- f(x) = {√(2x-1)} / 4
y = {√(2x-1)} / 4
4y = √(2x-1)
(4y)2 = 2x – 1
16y2 = 2x – 1
16y2 + 1 = 2x
(16y2 + 1) / 2 = x
f-1(x) = (16x2 + 1) / 2
then D(f-1) = all real numbers
- b(x) = 2x¾ + 1
y = 2x¾ + 1
y – 1 = 2x¾
(y – 1) / 2 = x¾
¾ √{(y-1)/2} = x
b-1(x) = ¾ √{(x-1)/2}
then D(b-1) = all real numbers x ≠ 1
3. If f(x) = 2x / (x+1) then f-1(3) = …
f(x) = 2x / (x+1)
y = 2x / (x+1)
xy + y = 2x
xy – 2x = -y
x(y-2) = -y
x = -y / (y-2)
f-1(x) = -x / (x-2)
then f-1(3) = -3 / (3-2) = -3
4. If g(x) = 2x – 1, h(x) = x2 + x – 1 then g-1(1) + g(0) – h(2) = …
Determine g-1(-1)
g(x) = 2x – 1
y = 2x – 1
y + 1 = 2x
x = (y+1) / 2
g-1(x) = (x+1) / 2
g-1(-1) = 0
Then
g-1(1) + g(0) – h(2)
0 + {2(0) – 1} – {22 + 2 – 1} = -6
5. If f-1(x) = x2 – 2x + 1 then f(1) = …
Remember concept {f-1(x)}-1 = f(x)
Then
f(x) = {f-1(x)}-1
replace f-1(x) with y
y = x2 – 2x + 1
y = (x – 1)2
√y = x – 1
√y + 1 = x
f(x) = √x + 1
so, f(1) = √1 + 1 = 2
