How move and resize the graphs of functions?
Example
f(x) = x2
Table of Contents
How move the graphs of functions?
- Add a constant to the y-value will move it up or down
- Add a constant to the x-value will move it left or right
Examples
| Function | c > 0 | c < 0 |
| f(x) = x2 g(x) = x2 + c | 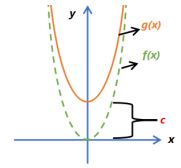 | 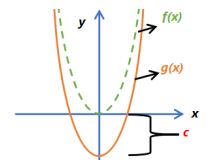 |
| f(x) = x2 g(x) = (x + c)2 | 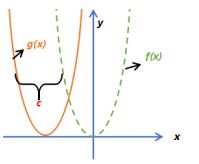 | 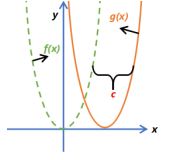 |
To put it simply:
- add to y to go high
- add to x to go left
How resize the graphs of functions?
- multiplying the whole function by a constant will stretch or compress it in the y-direction
- multiplying x by a constant will stretch or compress it in the x-direction
Examples
| Function | c > 1 | 0 < c < 1 |
| f(x) = x2 g(x) = cx2 | 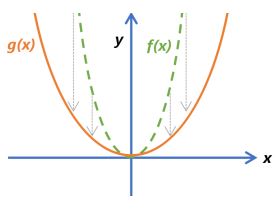 | 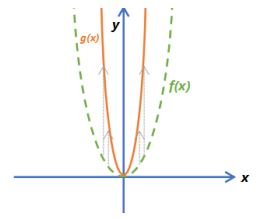 |
| f(x) = x2 g(x) = (cx)2 | 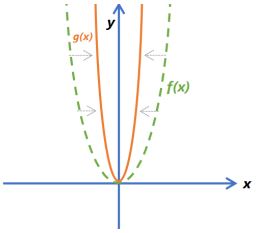 | 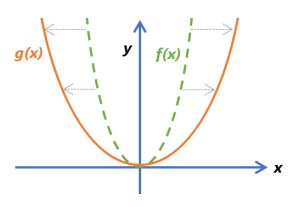 |
Note:
- for the y-direction, bigger values cause more stretch.
- for the x-direction, bigger c cause more compression.
How flip the graphs of functions?
- Multiplying the whole function by −1 will flip it upside down
- Multiplying the x-value by −1 will flip it upside down
| Function | Graph |
| f(x) = x2g(x) = -x2 | 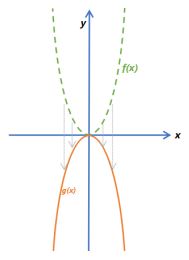 |
| f(x) = x2g(x) = (-x)2 | 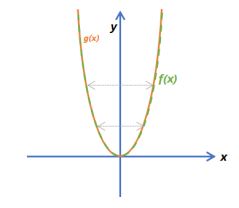 |
Summary
| y = f(x) + c | c > 0 moves it upc < 0 moves it down |
| y = f(x + c) | c > 0 moves it leftc < 0 moves it right |
| y = cf(x) | c > 1 stretches it in the y-direction0 < c < 1 compresses it |
| y = f(cx) | c > 1 stretches it in the x-direction0 < c < 1 stretches it |
| y = -f(x) | Reflects it about x-axis |
| y = f(-x) | Reflects it about y-axis |
All transformation in one go
To put it simply, use
a f(b(x + c)) + d
| Symbol | Detail |
| a | |a| > 1 stretches |a| < 1 compresses a < 0 flips the graph upside down |
| b | |b| > 1 compresses |b| < 1 stretches b < 0 flips the graph left-right |
| c | c < 0 shifts to the right c > 0 shifts to the left |
| d | d > 0 shifts upward d < 0 shifts downward |
