Table of Contents
Definition of Function
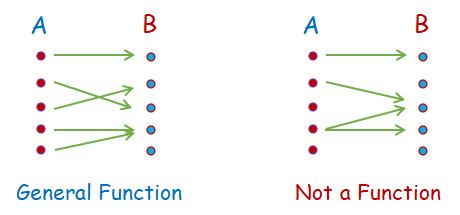
A General Function
- Points each member of “A” to a member of “B”.
- A member of “A” only points one member of “B”. (one-to-many is not allowed. Example: f(x) = 3 or 4 is not allowed)
- 2 or more members of “A” can point to the same “B” (many-to-one is allowed. Example: f(4) = f(5) = 4 is allowed)
Injective
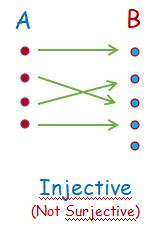
Injective means
- No 2 or more members of “A” point to the same “B”.
- Many-to-one is NOT allowed (Example: f(3) = f(4) = 2 is NOT allowed).
- One-to-many is NOT allowed too (Because it’s a function)
- Member(s) of “B” without a matching “A” is allowed
- Injective is also called “One-to-One“
A function f is injective if and only if whenever f(x) = f(y), x = y.
Surjective
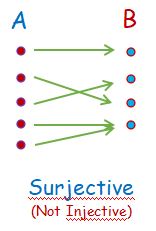
Surjective means
- Every member of “B” has at least 1 matching “A” (can has more than 1).
- Member(s) of “B” without a matching “A” is NOT allowed
f is surjective if and only if f(A) = B
A function f (from set A to B) is surjective if and only if for every y in B, there is at least one x in A such that f(x) = y
Bijective
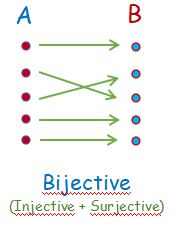
Bijective means
- Both Injective and Surjective together.
- A perfect “one-to-one correspondence” between the members of the sets. (Don’t get that confused with “One-to-One” used in injective).
A function f (from set A to B) is bijective if, for every y in B, there is exactly one x in A such that f(x) = y
Inverse
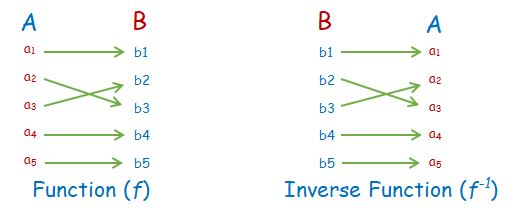
Bijective means
Bijection function is also known as invertible function because it has inverse function property.
It is a function which assigns to b, a unique element a such that f(a) = b. hence f-1 (b) = a.
