Table of Contents
Sequence
A Sequence is a set of things (usually numbers) that are in order.
1, 3, 5, 7, …
Each number in the sequence is called a term (or sometimes “element” or “member”).
Arithmetic Sequence
In an Arithmetic Sequence, the difference between one term and the next is called a constant.
In other words, we just add the same value each time infinitely.
2, 4, 6, 8, 10, 12, 14, 16, 18, …
This sequence has a difference of 2 between each number.
In General we could write an arithmetic sequence like this:
{a, a+d, a+2d, a+3d, … }
where:
- a is the first term
- d is the difference between the terms (called the “common difference”)
2, 5, 8, 11, 14, 17, 20, 23, …
Has:
a = 2 (the first term)
d = 3 (the “common difference” between terms)
And we get:
{a, a+d, a+2d, a+3d, … }
So
{2, 2+3, 2+2×3, 2+3×3, … }
{2, 5, 8, 11, … }
Rule
We can write an Arithmetic Sequence as a rule:
xn = a + d(n−1)
(We use “n−1” because d is not used in the 1st term).
Write a rule, and calculate the 10th term, for this Arithmetic Sequence:
5, 10, 15, 20, 25, …
This sequence has a difference of 5 between each number.
The values of a and d are:
a = 5 (the first term)
d = 5 (the “common difference”)
Using the Arithmetic Sequence rule:
xn = a + d(n−1)
xn = 5 + 5(n−1)
xn = 5 + 5n − 5
xn = 5n
So the 10th term is:
x10 = 5×10
x10 = 50
Summing an Arithmetic Series
To sum up the terms of this arithmetic sequence:
a + (a+d) + (a+2d) + (a+3d) + …
use this formula:
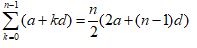
Here is how to use it:
Add up the first 10 terms of the arithmetic sequence:
{ 1, 5, 9, 13, 17, … }
The values of a, d and n are:
a = 1 (the first term)
d = 4 (the “common difference” between terms)
n = 10 (how many terms to add up)
So:
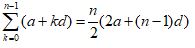
By subtitute the value of a, d, & n, we get