A fractional exponent is an alternate notation for expressing powers and roots together. Fractional Exponents are also known as Radicals or Rational Exponents.
Table of Contents
Whole Number Exponents
First, look at whole number exponents:
The exponent of a number says how many times to use the number in a multiplication.
62 = 6 × 6 = 36
43 = 4 × 4 × 4 = 64
In words:
62 could be called “6 to the second power”, or “6 to the power 2” or simply “6 squared”
Fractional Exponents
Remember that when aa is a positive real number, both of these equations are true:
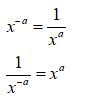
If the exponent is a fraction?
When you have a fractional exponent, the numerator is the power and the denominator is the root. In the variable. So:
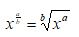
Where:
- x is a real number
- a and b are positive real numbers
- a is the power
- b is the root
| Exponent of Fraction | Example |
| An exponent of ½ is square root | |
| An exponent of ⅓ is cube root | |
| An exponent of ¼ is 4th root | |
| And so on! | etc |
General Rule
It worked for ½, it worked with ¼, in fact it works generally:
x1/n = The n-th Root of x
So we can come up with this
A fractional exponent like 1/n means to take the n-th root:
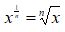
What is 81/3 ?
Answer:
81/3 = 3√8 = 2
More Complicated Fractions
What about a fractional exponent like 93/2 ?
That is really saying to do a cube (3) and a square root (1/2), in any order.
A fraction (like m/n) can be broken into two parts:
- a whole number part (m) , and
- a fraction (1/n) part
So, because m/n = m × (1/n) we can do this:
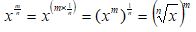
And we get this:
A fractional exponent like m/n means:
| In Symbols | Example | |
| Do the m-th power, then take the n-th root | 93/2 = 2√(93) = 2√729 = 27 | |
| Or Take the n-th root and then do the m-th power | 93/2 = (2√9)3 = 33 = 27 |
If they give you x3/6, then x had better not be negative, because x3 would still be negative, and you would be trying to take the sixth root of a negative number.
If they give you x4/6, then a negative x becomes positive (because of the fourth power) and then it is sixth-rooted, so by reducing the fractional power it becomes |x|2/3.
But, if they give you something like x4/5, then you don’t need to care whether x is positive or negative, because a fifth root doesn’t have any problem with negatives.
