Table of Contents
Definition
The exponent of a number says how many times to use the number in a multiplication.
In 42 the “2” says to use 4 twice in a multiplication,
so
42 = 4 × 4 = 16
In words:
42 could be called “4 to the power 2” or “4 to the second power”, or simply “4 squared”
Exponents are also called Powers or Indices.
Some more examples:
| In Numbers | In Words |
| 33 = 3 × 3 × 3 = 27 | “3 to the third power”, “3 to the power 3”,or simply “3 cubed” |
| 54 = 5 × 5 × 5 × 5 = 625 | “5 to the fourth power”,”5 to the power 4″, or simply “5 to the 4th” |
Exponents make it easier to write and use many multiplications
76 is easier to write and read than 7 × 7 × 7 × 7 × 7 × 7
We can multiply any number by itself as many times as we want using exponents.
In General
an tells you to multiply a by itself, so there are n of those a‘s:
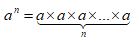
If the Exponent is 1 or 0?
| Exponent | Answer | Example |
| 1 | number itself | 81 = 8 |
| 0 | 1 | 60 = 1 |
What about 00 ?
It could be either 1 or 0, and so people say it is “indeterminate“.
Negative Exponents
What could be the opposite of multiplying?
Dividing!
A negative exponent means how many times to divide one by the number.
4-1 = 1 ÷ 4 = 0.25
You can have many divides
10-2 = 1 ÷ 10 ÷ 10 = 0.01
That can be done in another way:
10-2 could also be calculated like:
1 ÷ (10 × 10) = 1/102 = 1/100 = 0.01
Negative Exponent = Flip the Positive Exponent
That last example showed an easier way to handle negative exponents:
- Calculate the positive exponent (an)
- Then take the Reciprocal (1/an)
More Examples:
| Negative Exponent | Reciprocal of Positive Exponent | Answer |
| 5-2 | 1/52 | 1/25 = 0.04 |
| 2-3 | 1/23 | 1/8 = 0.125 |
| (-10)-3 | 1/(-10)3 | 1/(-1000) = -0.001 |
Makes Sense
Start with “1” and then multiply or divide as many times as the exponent says, then you will get the right answer.
Example
| etc… | n-2 | n-1 | Number (n) | n1 | n2 | etc… |
| … | 2-2=1÷2÷22-2=0.25 | 2-1 = 1÷22-1 = 0.5 | 2 | 21 = 1×221 = 2 | 22=1×2×222=4 | … |
| … | 4-2=1÷4÷44-2=0.0625 | 4-1 = 1÷44-1 = 0.25 | 4 | 41 = 1×441 = 4 | 42=1×4×442=16 | … |
| … | 5-2=1÷5÷55-2=0.04 | 5-1 = 1÷55-1 = 0.2 | 5 | 51 = 1×551 = 5 | 52=1×5×552=25 | … |
Another Way of Writing Exponent
Sometimes people use the ^ symbol (above the 6 button on your keyboard), as it is easy to type.
3^2 is the same as 32
3^2 = 3 × 3 = 9
About Grouping
To avoid confusion, use parentheses () in cases like this:
| With ( ) | Without ( ) |
| (-7)2 = (-7) × (-7) = 49 | -72 = -(72) = – (7 × 7) = -49 |
| (ab)2 = ab × ab | ab2 = a × (b)2 = a × b × b |
