Table of Contents
Definition of Logarithmic Functions
Logarithmic and exponential function has close relation. It is because logarithmic inverse of exponential function.
Any exponential function can be changed to be logarithmic function and any logarithmic function can be changed to be exponential function.
For example there is exponential function x = ay, so the logarithmic function is alog x = y or can be written as loga x = y (read it as log base a to x).
In another words, it can said that logarithmic function is determining process to get the power of a value.
Another example is 10x10x10x10 = 104 or it is said 104 = 10000 in exponent function. But in logarithmic function, it will be 10log10000 = 4 or can be written log1010000 = 4.
But there is special for base 10. It just write as log10000 = 4.
So, based on the example, logarithmic function is
If there is ay = x is equivalent with y = logax or y = alogx
Note: a is any number such that a>0, a≠1, and x>0.
Logarithmic Rules
Remembering the concept of exponent and logarithmic, there are logarithmic rules:
1. Logbb = 1
It’s because b1 = b
2. Logb1 = 0
It’s because b0 = 1
3. Logbbx = x
It’s because bx = bx
4. 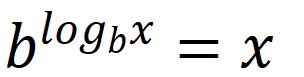
It’s because logbx = logbx
There are also onther rules that based on exponent and logarithmic concept and the operation.
5. Logb(MN) = logbM + logbN (product rule)
6. Logb(M/N) = (logbM)/(logbN) (division rule)
7. LogbMx = x. logbM (power rule)
8. If logbM = logbN then M = N (equality rule)
9. logbM = (log M)/(log b)
Logarithmic Examples
Solve the following problems:
- if Logy8 = 3 then determine the value of y!
Based on the concept of logarithmic,
Logy8 = 3 means y3= 8 Þy = 2
2. if Log2(1/8) = y then determine the value of y!
Log2(1/8) = y means 2y = 1/8 Þ y = -3 it is because 2-3 = 1/8
3. If Log 3 = 0.477 and log 2 = 0.301, then log 18 = …
Log 18 = log (2.9)
= log (2. 3. 3)
= log 2 + log 3 + log 3 (remember the rule)
= 0.301 + 0.477 + 0.477
= 1.255
4. 2 . log616 – 3 . Log64 + log69 = …
2 . log616 – 3 . Log64 + log69 = 2. log624 – 3. Log622 + log632 (remember the rules)
= log628 – log626 + log632
= log6((28/26).32)
= log6(36)
= 2 (because 62 = 36)
5. If log35 = a and log57 = b, then determine log7225 = …
First step: determine logarithm that we need to solve the problem.
log35 = a Þ (log 5)/(log 3) = a Þ log 3 = (1/a). log 5.
Log57 = b Þ (log 7)/(log 5) = b Þ log 7 =b. log 5.
Second step: use log 7 and log 3 and substitute to the problem
Log7225 = (log 225)/(log 7)
= (log 52.32)/(log 7)
= (log 52 + log 32)/(log 7)
= (2.log 5 + 2.log 3)/log 7
= (2.log 5 + 2.(1/a)log 5)/b.log 5 (substitute the value from step 1)
= ((2+(2/a)).log 5) /b.log 5 (eliminate log 5)
= (2a+2)/a . (1/b)
=(2a+2)/ab
