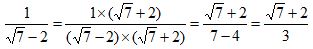Table of Contents
Irrational Denominator
Denominator: the bottom number of fraction
Rational: Numbers such as 2, 3, 7
Irrational: Roots such as √2, √3, √7
The Irrational Denominator of ![]()
Simplest form of number cannot have the irrational denominator.
To be in simplest form, Rationalizing the Denominator!
Rationalizing the Denominator is making the denominator rational
How to Rationalizing the Denominator
Rationalizing the Denominator With 1 Term
Step 1: Multiply numerator and denominator by a radical.
- If the radical in the denominator is a square root, then you multiply by a square root that will give you a perfect square under the radical when multiplied by the denominator.
- If the radical in the denominator is a cube root, then you multiply by a cube root that will give you a perfect cube under the radical when multiplied by the denominator.
- and so on …
Note: that the phrase “perfect square” means that you can take the square root of it. Just as “perfect cube” means we can take the cube root of the number, and so forth.
Keep in mind that as long as you multiply the numerator and denominator by the exact same thing, the fractions will be equivalent.
Step 2: Make sure all radicals are simplified
Some radicals will already be in a simplified form, but make sure you simplify the ones that are not.
Step 3: Simplify the fraction if needed.
Be careful! You cannot cancel out a factor that is on the outside of a radical with one that is on the inside of the radical.
In order to cancel out common factors, they have to be both inside the same radical or be both outside the radical.
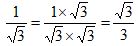
Rationalizing the Denominator With 2 Term
We talked about rationalizing the denominator with 1 term above. When we have 2 terms, we have to approach it differently than when we had 1 term.
Step 1: Find the conjugate of the denominator
Find the conjugate of a binomial by changing the sign that is between the 2 terms, but keep the same order of the terms.
Ex: a + b and a – b are conjugates of each other.
Step 2: Multiply the numerator and denominator by the conjugate
Keep in mind that as long as you multiply the numerator and denominator by the exact same thing, the fractions will be equivalent.
Step 3: Make sure all radicals are simplified
Some radicals will already be in a simplified form, but make sure you simplify the ones that are not.
Step 4: Simplify the fraction if needed
Remember! You cannot cancel out a factor that is on the outside of a radical with one that is on the inside of the radical.
To cancel out common factors, they have to be both outside the same radical or be both inside the radical.