A quadratic is a type of problem In mathematics that deals with a variable multiplied by itself (an operation known as squaring).
It derives from the area of a square being its side length multiplied by itself. The word quadratic comes from “quadratum”, which means square in Latin word.
There are a lot of phenomena in the real world that can be described by Quadratic equations. For example is rocket fly route, where it will land, how long it will take a person to row down & up a river, or how much to charge for a product.
Because of these applications, quadratics equations have profound historical importance and were foundation of algebra.
Table of Contents
Quadratic Equation
Only if it can be put in the form ax2 + bx + c = 0, and a is not zero.
The name comes from “quad” meaning square, as the variable is squared (in other words x2).
These are all quadratic equations in disguise:
| Equation | In standard form | a, b and c |
| x2 = x + 1 | x² -x – 3 = 0 | a=1, b=-1, c=-3 |
| 2(x2 – 2x) = 2 | 2x² – 4x – 2 = 0 | a=2, b=-4, c=-2 |
| x(x-6) = 18 | -x² +6x + 18 = 0 | a=-1, b=6, c=18 |
| 20 – 15/x – 10/x2 = 0 | 20x² -15x – 10 = 0 | a=20, b=-15, c=-10 |
Quadratic Formula
How Does this Work?
The solution(s) to a quadratic equation can be calculated using the Quadratic Formula:
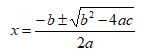
The “±” means we need to do a plus AND a minus, so there are normally TWO solutions !
The part (b2 – 4ac) is called the “discriminant“, because it can “discriminate” between the possible types of answer:
- when b2 – 4ac > 0, we get two real solutions,
- when b2 – 4ac = 0, we get just ONE solution,
- when b2 – 4ac < 0, we get complex solutions.
Find x !
| Equation | a, b and c | Operation | x |
| x² -x – 3 = 0 | a=1, b=-1, c=-3 | 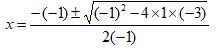 | 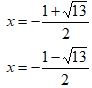 |
| 2x² – 4x – 2 = 0 | a=2, b=-4, c=-2 | 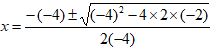 | 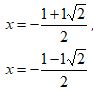 |
In order to Quadratic Formula to work, you must have your equation arranged in the form:
(quadratic) = 0
Also, the 2a in the denominator of the Formula is not just the square root. It is underneath everything above.
Make sure not to drop the square root or the “±” in the middle of your calculations, so you will not need to put them back in.
Remember that b2 means “the square of ALL of b, including its sign”. Do not leave b2 being negative, even if b is negative, because the square of a negative is a positive.
In other words, don’t be sloppy and don’t try to take shortcuts, because it will only hurt you in the long run. Trust me on this!
Examples
1. Solve the quadratic equation by factorization method:
a. x2 – 4x – 12 = 0
b. m2 = -6m – 5
a. x2 – 4x – 12 = 0
it can be solved by using factorization.
x2 – 4x – 12 = 0
→ (x-6)(x+2) = 0
→ x1 = 6
→ x2 = -2
b. m2 = -6m – 5
m2 + 6m + 5 = 0 (using factorization)
→ (m+5)(m+1) = 0
→ m1 = -5
→m2 = -1
2. Solve the quadratic equations:
a. 2x2 – 3x -2 = 0
b. k(k+2) + 2 = 0
c. (k-2)2 – 36 = 0
a. 2x2 – 3x -2 = 0
x1,2 = {-b ± √(b2-4ac)} / 2a
= {3 ± √(9-4.2.(-2))} / 2.2
= {3 ± √25} / 4
= {3 ± 5} / 4
x1 = 8/4
x2 = -2/4 = – ½
b. k(k+2) + 2 = 0 → k2 + 2k +2 = 0
x1,2 = {-b ± √(b2-4ac)} / 2a
= {-2 ± √(4-4.1.(2))} / 2.1
= {-2 ± √-4} / 2
= {-2 ± 2√-1} / 2
= {-2 ± 2i}/2
= -1 ± i
x1 = -1 + i
x2 = -1 – i
c. (k-2)2 – 36 = 0 → k2 -4k + 4 -36 = 0 → k2 – 4k – 32 = 0
x1,2 = {-b ± √(b2-4ac)} / 2a
= {4 ± √(16-4.1.(-32))} / 2.1
= {4 ± √144} / 2
= {4 ± 12} / 2
= 2 ± 6
x1 = 8
x2 = -4
3. solve the quadratic equation in fraction forms:
a. {(x2-10)/x+2} + x – 1 = x
b. y + 1 = {(2y–7)/(y+5)} – {(5y+8)/(y+5)}
a. {(x2-10)/x+2} + x – 1 = x
→ {(x2-10)/x+2} = 1 + x – x
{(x2-10)/x+2} = 1
{(x2-10)/x+2} (x+2) = 1 (x+2) (simplify by multiplying the denominator)
x2 – 10 -x- 2 = 0
x2 – x- 12 = 0
(x+3)(x-4) = 0
x1 = -3
x2 = 4
b. y + 1 = {(2y–7)/(y+5)} – {(5y+8)/(y+5)}
y + 1 = {(2y–7-(5y+8))/(y+5)}
y + 1 = {(2y–7-5y-8))/(y+5)}
y + 1 = {(-3y–15)) / (y+5)}
(y + 1)(y+5) = {(-3y–15)) / (y+5)} (y+5) (simplify by multiplying the denominator)
y2 + 6y + 5 = -3y – 15
y2 + 9y + 20 = 0
(y+4)(y+5) = 0
x1 = -4
x2 = -5
4. Alex has some box of candies. In mathematics form, it is x2 – 2x – 3 = 0. x as a box that contain some candies. If he bought a candy $0.5 then how much he did paid if he only bought 4box?
Candies x2 – 2x – 3 = 0, x as the box that contain some candies.
First step is determining how many candies in a box. In another words, we must determine the value of x.
x2 – 2x – 3 = 0
(x-3)(x+2) = 0
x1 = 3
x2 = -1
(it is impossible x = -1 because of the content is candy. It is impossible if it minus / negative)
Next, each candy is $0.5. So, if Alex bought 4box means 4x = 4 (3) = 12 candies.
The price is 12 x (0.5) = $6.
