Mathematics identic with numbers. Some of them have special pattern. It is not only arithmetic and geometry sequences but also truly special pattern. One of them is Pascal’s triangle.
In real life it can be applied to solve combination of head and tail problems, polynomials problem (binomial expansion), etc..
Table of Contents
Definition of Pascal’s Triangle
Pascal’s triangle was named by a French mathematician, Blaise Pascal (1623-1662). It is one of mathematics concept in algebra. Pascal’s triangle is binomial coefficient (number pattern) in triangle array.
Pascal’s Triangle pattern
There are some patterns of Pascal’s triangle.
1. Diagonal patterns
There are 6 rows of Pascal’s triangle. Look at the diagonals of Pascal’s triangle.
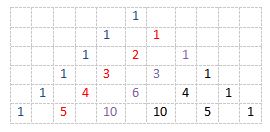
- First diagonal is always “1” (the blue ones)
- Second diagonal is counting numbers “1,2,3,…” (red ones)
- Third diagonal is triangular numbers “1,3,6,…”(purple ones)
2. Fibonacci sequences
Fibonacci sequences is 0, 1, 1, 2, 3, 5, 8, … Pascal’s triangle has it in addition some of the numbers.
Starting with 0, then Pascal’s triangle has the remainder.
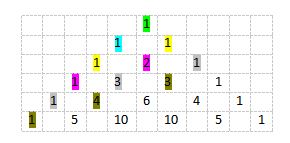
Look at each color. Add the numbers that have same color.
1
1
1 + 1 = 1
1 + 2 = 3
1 + 3 + 1 = 5
1 + 4 + 3 = 8
…
It will be Fibonacci sequences.
3. Squares
Look at the second diagonal of Pascal’s triangle.
The square of the numbers is equals to addition the numbers next to it and below.
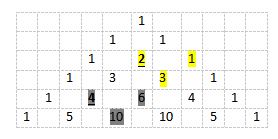
Some of the squares are
22 = 4 = 3 + 1
42 = 16 = 10 + 6
4. Exponents of 11
Look at each row. It is the result of exponents (power) of 11.
110 = 1
111 = 11
112 = 121
113 = 1331
114 = 14641
But 115 ≠ 15101051.
115 = 161051. It is because 15101051 has more digit numbers. Then it must be 1(5+1)(0+1)051 = 161051.
It also has same concept to 116 and bigger power.
5. Horizontal sum
Pay attention in each row.
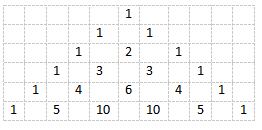
Each row is the result of 2n.
20 = 1
21 = 2 = 1+ 1
22 = 4 = 1 + 2 + 1
23 = 8 = 1 + 3 + 3 + 1
24 = 16 = 1 + 4 + 6 + 4 + 1
25 = 32 = 1 + 5 + 10 + 10 + 5 + 1
6. Symmetrical numbers
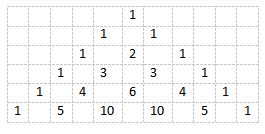
Another pattern of Pascal’s triangle is symmetrical number between left and right side. Look at the triangle and see how the mirror of the numbers.
Pascal’s Triangle formula
Pascal’s triangle has many numbers. If there are five rows you can determine the numbers in 8th rows or others. It uses the formula (combination concept).

Note:
- n : row
- r : term / element, 0 ≤ r ≤ n
if there are only six rows then the problem is determining the number in 10th row term 4,
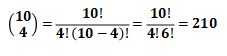
Triangle array in Pascal’s triangle is arranged by summing adjacent elements in previous row. It starts with “1” in zero row then continued with 1 and 1 in first row. Second row is addition of number in first row and continued with same step in next row.
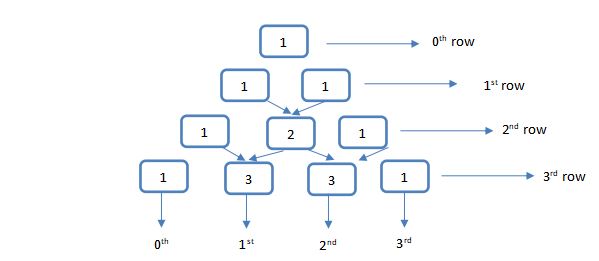
Why there is 0th?
The reason is making Pascal’s triangle (elements in the array) correspond to binomial coefficients.
Pascal’s triangle relates to polynomial. It is as coefficient of binomial expansion.
- (x+1)2 = 1x2 + 2x + 1x0 = x2 +2x + 1
- (x+1)3 = 1x3 + 3x2 + 3x + 1x0 = x3 + 3x2 + 3x + 1
- (x+1)4 = 1x4 + 4x3 + 6x2 + 4x + 1x0 = x4 + 4x3 + 6x2 + 4x + 1
- Etc.
Look at the power and the pascal’s triangle. The power shows the number of rows of pascal’s triangle.
Examples
1. Determine the value of
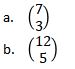
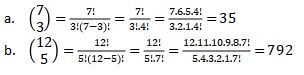
2. What is row 15, term 3 in Pascal’s triangle?
Row 15 term 3 means
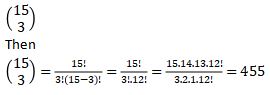
3. What is the binomial expansion of (x+1)6?
Using pascal’s triangle in 6th row that is 1 6 15 20 15 6 1 then
(x+1)6 = 1x6 + 6x5 + 15x4+ 20x3 + 15x2 + 6x + 1
= x6 + 6x5 + 15x4+ 20x3 + 15x2 + 6x + 1
4. What is the binomial expansion of (m+2)5?
Using pascal’s triangle in 5th row.
1 5 10 10 5 1
and
(a+b)5 = 1a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + 1b5
Then
(m+2)5 = 1m5 + 5m4(2) + 10m3(2)2 + 10m2(2)3 + 5m(2)4 + 1(2)5
= 1m5 + 10m4 + 40m3 + 80m2 + 80m + 32
5. What is the binomial expansion of (a-2)7?
Using 7th row
1 7 21 35 35 21 7 1
then
(a-2)7 = 1a7 + 7a6.(-2) + 21a5.(-2)2 + 35a4.(-2)3 + 35a3.(-2)4 + 21a2.(-2)5 + 7a.(-2)6 + 1.(-2)7
= a7 – 14a6 + 84a5 – 280a4 + 140a3 – 672a2 + 448a – 14
