Table of Contents

What is Hyperbolic functions?

Hyperbolic function identic with trigonometry function especially sine and cosines. It is exponential functions that has properties like trigonometry.

The basic of hyperbolic functions are hyperbolic sine and cosines. But the both of them are different with sine and cosines in trigonometry.

In real life, it can be applied to determine the curve that made by suspended cable or other things. The curve that is formed by the hanging cable called catenary. It uses cosh function (f(x) = a.cosh(x/a).

More detail about basic of hyperbolic functions are:

Hyperbolic sine (sinh)

Sinh (x) = (e^{^x} – e^{^-x}) / 2

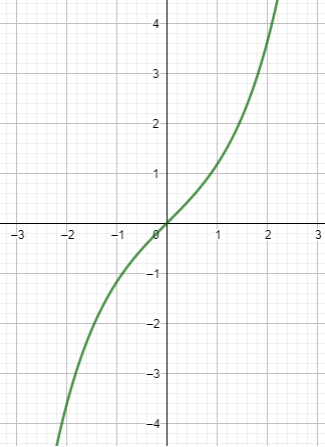
Hyperbolic cosine (cosh)

Cosh (x) = (e^{^x} + e^{^-x}) / 2

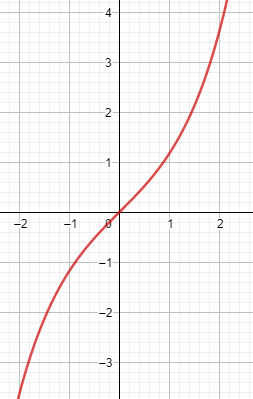
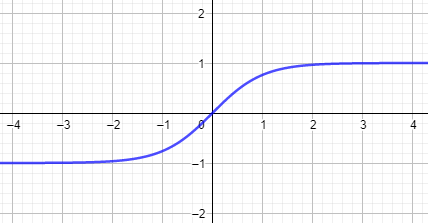
Because of them, there are other of basic hyperbolic functions, they are:

Hyperbolic tangent (tanh)

Tanh(x) = {sinh (x)} / {cos (x)} = (e^{^x} – e^{^-x}) / (e^{^x} + e^{^-x}) = {e^{^2x}-1} / {e^{^2x}+1}

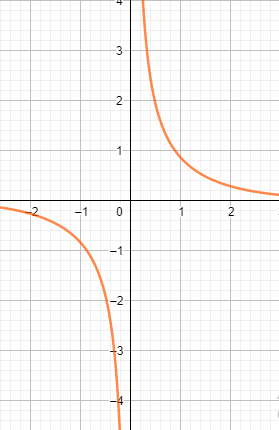
Hyperbolic cosecant (csch)

Csch (x) = 1/sinh(x) = {2^{^ex}} / {e^{^2x}-1}

Hyperbolic secant (sech)

Sech (x) = 1/cosh(x) = {2^{^ex}}/{e^{^2x}+1}

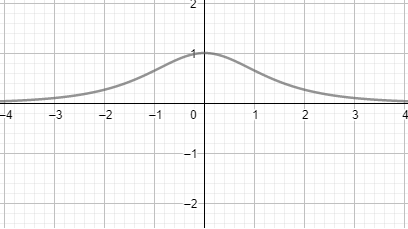
Hyperbolic cotangent (coth)

Coth(x) = 1/tanh(x) = {e^{^2x}+1} / {e^{^2x}-1}

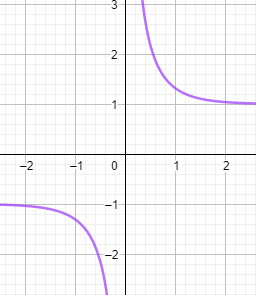
Inverse of Hyperbolic functions

The inverses of hyperbolic functions are:

Hyperbolic sines denoted as sinh^-1 or arsinh or arcsinh

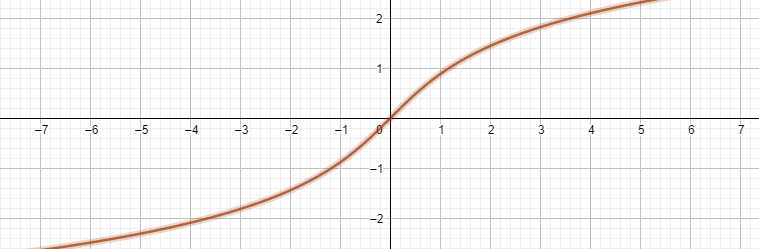
Hyperbolic cosine denoted as cosh^-1 or arcosh or arccosh

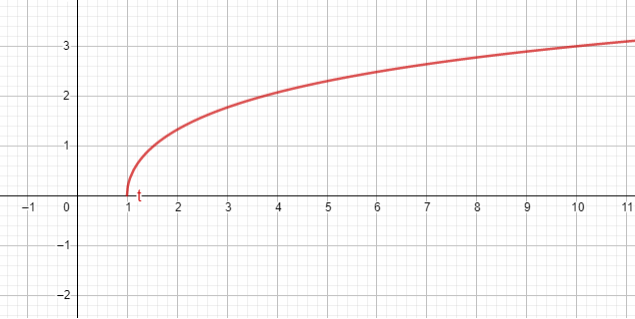
The other invers of hyperbolic function are (please check the graph by yourself)

Hyperbolic tangent denoted as tanh^-1 or artanh or arctanh
Hyperbolic cosecant denoted as csch^-1 or arcsch or arccsch
Hyperbolic secant denoted as sech^-1 or arsech or arcsech
Hyperbolic cotangent denoted as coth^-1 or arcoth or arccoth

Identities of Hyperbolic Function

in hyperbolic function, there are identities:

Sinh (-x) = – sinh (x)
Cosh (-x) = cosh (x)
Tanh (-x) =- tanh (x)
Coth (-x) = – coth (x)
Sech (-x) = sech (x)
Csch (-x) = – csch (x)

Derivatives of Hyperbolic Function

Derivatives of hyperbolic function are:

d/dx {sinh (x)} = cosh (x)
d/dx {cosh(x)} = sinh (x)
d/dx {tanh (x)} = 1 – tanh²(x) = sech²x = 1 / {cosh²(x)}
d/dx {coth(x)} = 1 – coth²(x) = – csch²(x) = – 1 / {sinh²(x)}
d/dx {sech(x)} = -tanh(x) . sech(x)
d/dx {csch(x)} = -coth(x) . csch(x)
d/dx {arcsinh(x)} = 1 / √(x²+1)
d/dx {arcosh(x)} = 1 / √(x²-1) for x>1

Hyperbolic Function Examples

Differentiate y = cosh (√x).

Example

using derivative properties and chain rule, it will be

d/dx {cosh (√x)} = sinh (√x) . {1 / (2√x)}

= {sinh (√x)} / {2√x}

2. Determine the derivative of f(x) = tan(5x).

Example

f(x) = tan(5x)

f’(x) = 5. {sech²(5x)}

3. Determine the derivative of y = x². Sinh^-1(3x).

Example

Using derivative properties for f(x) = u.v then f’(x) = u’v + uv’

y = x². Sinh^-1(3x)

y’ = 2x. Sinh^-1(3x) + x².{1 / √(1+(3x)²)}.3

= 2x.{sinh^-1(3x) + x/√(1+9x²)}