Table of Contents
Right Triangle
The Trigonometric Identities are equations that are true for Right Angled Triangles.
Each side of a right triangle has a name:
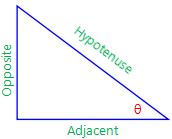
- Adjacent is always next to the angle
- Opposite is opposite the angle
Sine, Cosine and Tangent
3 main functions in trigonometry are Sine, Cosine and Tangent. They are just the length of one side divided by another
For a right triangle with an angle θ :
| Sine Function | sin(θ) = Opposite / Hypotenuse |
| Cosine Function | cos(θ) = Adjacent / Hypotenuse |
| Tangent Function | tan(θ) = Opposite / Adjacent |
For a given angle θ each ratio stays the same no matter how big or small the triangle is.
When we divide Sine by Cosine we get:
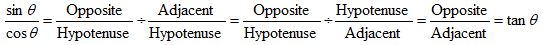
So we can say:
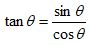
Cosecant, Secant and Cotangent
We can also divide “the other way around” (such as Adjacent/Opposite instead of Opposite/Adjacent):
| Cosecant Function | csc(θ) = Hypotenuse / Opposite |
| Secant Function | sec(θ) = Hypotenuse / Adjacent |
| Cotangent Function | cot(θ) = Adjacent / Opposite |
when Opposite = 1 and Hypotenuse = 2 then
sin(θ) = 1/2, and
csc(θ) = 2/1
Because of all that we can say:
sin(θ) = 1/csc(θ)
cos(θ) = 1/sec(θ)
tan(θ) = 1/cot(θ)
And the other way around:
csc(θ) = 1/sin(θ)
sec(θ) = 1/cos(θ)
cot(θ) = 1/tan(θ)
Pythagoras Theorem
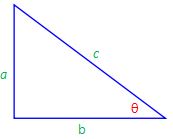
For the next trigonometric identities we start with Pythagoras’ Theorem:
The Pythagorean Theorem says that, in a right triangle, the square of a plus the square of b is equal to the square of c:
a2 + b2 = c2
Dividing through by c2 gives
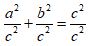
This can be simplified to:
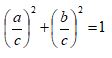
- a/c is Opposite / Hypotenuse, which is sin(θ)
- b/c is Adjacent / Hypotenuse, which is cos(θ)
So (a/c)2 + (b/c)2 = 1 can also be written:
sin2 θ + cos2 θ = 1
Note:
sin2 θ means to find the sine of θ, then square the result, and
sin θ2 means to square θ, then do the sine function
Related identities
Related identities include
sin2 θ = 1 − cos2 θ
cos2 θ = 1 − sin2 θ
tan2 θ + 1 = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
Opposite Angle Identities
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
Double Angle Identities
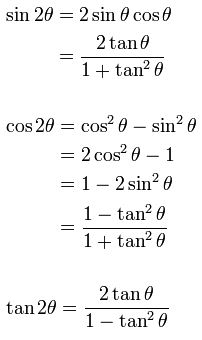
Half Angle Identities
Note that “±” means it may be either one, depending on the value of θ/2
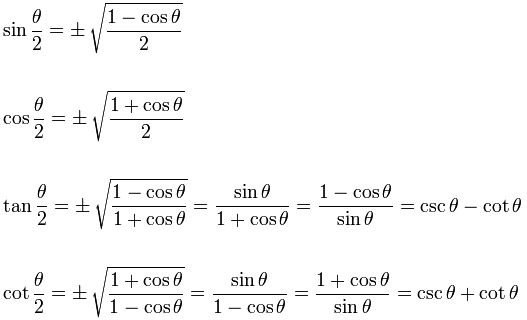
Angle Sum and Difference Identities
| Sine | sin (A+B) = sin A cos B + cos A sin B sin (A-B) = sin A cos B – cos A sin B |
| Cosine | cos (A+B) = cos A cos B – sin A sin B cos (A-B) = cos A cos B + sin A sin B |
| Tangent | 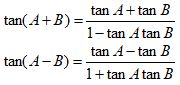 |
| Cotangent | 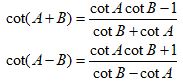 |
