Triangle has been used since long time ago in human life. There are many things in daily life that has triangle in shape for example ruler, hanger, slice of sandwich, front and back side of tent, surface of pyramid, etc..

Table of Contents

Definition of Triangles

Triangles is a two-dimension shape that bordered by three sides so that it has three angles. Sum of the angles is 180°. Triangle has some type that based on the sides and the vertex (angles). Triangle is also

Properties of a Triangles

1. Sum of interior angles is 180°

If there are α, β, and g as the interior angles then α + β + g = 180°.

2. Sides of the triangle has special properties (triangle inequality theorem)

The theorem is sum of two any sides of triangles is more than the third side.

If there are a, b, and c as the sides, then

a + b > c

a + c > b

b + c > a

3. The largest angle is in opposite of the largest sides and the smallest angle is opposite of the smallest side.

4. The exterior angle (q) of triangle is sum of the remote interior angles (α and β).

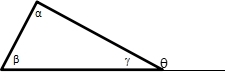
q = α + β

Type of Triangle

Based on the type of triangle’s side, there are three types of triangles:

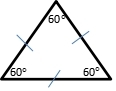
Equilateral Triangle

Equilateral comes from “equal” means same measure. Equilateral triangle has same length of the sides. Besides that, it also has same measure of the angles. Each of them is 60° then the sum is 180°.

Isosceles Triangle

Isosceles triangle only has two sides in same length. Then they are called it as “feet”. Because of it has only two same sides in length, consequently it has two same measure of angle in the corner (vertex).

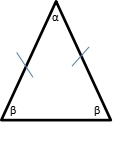
Sum of α + β + β = 180°

Scalene Triangle

Scalene triangle has no same length sides. It has three different length in the sides. Furthermore, it has three different measure of the angles.

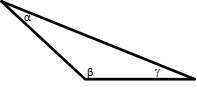
Sum of α + β + g = 180°

Based on the type of triangle’s angle, there are three types of triangles:

Right Triangle

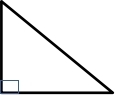
Right triangle means triangle that has one 90° in the corner/vertex. Because of sum of angles of the triangle is 180°, then there is impossible that has two right angles.

Acute Triangle

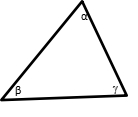
Acute triangle is triangle that has acute angles in all of the vertex. Based on the illustration, α β g are acute angles and sum of them is 180°. It is impossible that one of them is isosceles triangle because of it has 60° in each vertex. In another words, scalene triangle is also can be one of them.

Obtuse Triangle

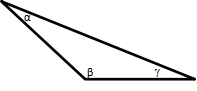
Obtuse triangle means triangle that has obtuse angle in one of the vertexes. Consequently, the other vertex are acute angles. It is because sum of them is 180°. Based on the illustration, if β is obtuse angle, then α, g are acute angles. Scalene triangle can be one of them.

Based on the both different base of triangle’ types, it is possible that a triangle has two types of triangle combine between based on the sides and the angle for example “right isosceles triangle”.

There is special case in triangle. It is based on the angles. There are two special case that based on the Pythagorean Theorem. What is Pythagorean Theorem?

Pythagorean theorem used to determine the hypotenuse of right triangle (or other side).

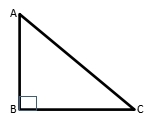
AC^² = AB^² + BC^²

The Special Triangles

1. 45-45-90

It means the triangle has angle 45°, 45°, and 90°. Based on the properties, it can be concluded that it is isosceles right triangle. The triangle is called special because of it has ratio of the sides. It will help to determine the length of the sides. The ratio is AB : BC : AC = 1 : 1 : √2.

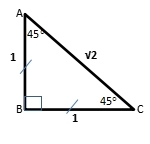
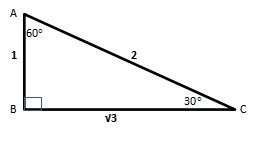
2. 30-60-90

Another special triangle is triangle that has angle 30°, 60°, and 90°. It also has ratio in the sides. AB : BC : AC = 1 : √3 : 2.

Area of a Triangles

Area of triangle is plane that bordered by three sides. Eventhough triangles have some types, the area is only one concept. It is a half of multiplication of the base and height.

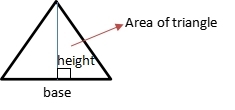
Area = A = ½ x base x height = ½ x b x h

But in another case, there is scalene triangle or another triangle that make it hard to determine the height.

Other concept to determine the area is using trigonometry concept.

Triangle that is known the length of two sides and the angle in between of them (S-A-S).

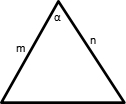
Area = ½ x m x n sinα

SAS method is also can be applied in other pairs of sides and angles.

Triangle that is known the two angles and length of the side in between of them (A-S-A).

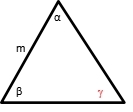
Area = (m^² x sin α x sin β) / (2 x sin g)

It is also can be applied in other pairs of sides and angles.

Note: if a triangle known the two angles, then the third can be determine by using concept that sum of the interior angles is 180°.

Triangle that is known all of the sides (S-S-S)

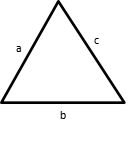
Area = A = √s(s-a)(s-b)(s-c)

(Heron’s Fromula)

Where s is half of the perimeter.

s = ½ (a+b+c)

When we know 3 sides of the triangle, we can also find the missing angles using SSS Method.

Perimeter of a Triangles

Perimeter means total length of triangle’s sides. In another word, the concept is sum of all sides.

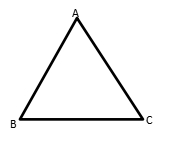
Perimeter = P = AB + BC + AC

Concept of perimeter can be applied in all type of triangle. But, in some case, the first step is determining the length of the side (sometime it use Pythagorean theorem).

Examples

1. Which statement is true about triangle?

a. It has total angle 360°
b. The smallest angle is in front of shortest side.
c. There is impossible obtuse equilateral triangle.

Answer

a. False, the total angle of triangle is 180°.

b. True, it is also the largest angle is in front of the largest side (longest side).

c. True, because obtuse angle means it is more than 90° but the equilateral triangle means all sides are same in length that consequently each angle is 60°.

2. Determine which set that can be a triangle

a. 4, 5, 8
b. 6, 8, 10
c. 7, 2, 1

Answer

Look at the properties. Sum of any two sides is more than the third side, then

a. 4 + 5 > 8 (can be a triangle)

b. 6 + 8 > 10 (can be a triangle)

c. 1 + 2 < 7 (it cannot be a triangle)

3. Determine the value of x, y, and z

Answer

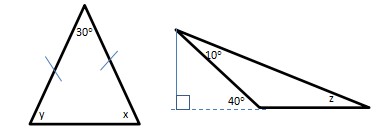
Look at the first triangle to determine x and y.

It is isosceles triangle so that it has same measurement of the angles in the bottom, x = y.

Because of total angles is 180°, then

30° + x + y = 180°

30° + x + x = 180°

30° + 2x = 180°

2x = 150°

x = 75°, so y = 75°

Then look at the second triangle to determine z.

Look at the unknown angle that is supplementary angle of 40°. It means 180° – 40° = 140°.

Next, using total angle of triangle

10° + 140° + z = 180°

150° + z = 180°

z = 30°

4. Determine the value of m+n

Answer

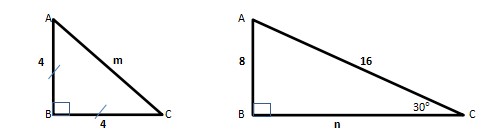
Eventhough the picture is not complete yet; it can be said that first picture is 45-45-90 and second is 30-60-90. Why?

First picture

It is known that it is isosceles right triangle, then the other angles are (180 – 90)/2 = 45°.

Then the ratio is AB : BC : AC = 1 : 1 : √2 → AB : BC : AC = 4 : 4 : 4√2

m = 4√2

Second picture

The third angle is 180° – 90° – 30° = 60°, so it has ratio

AB : BC : AC = 1 : √3 : 2 → AB : BC : AC = 8 : 8√3 : 16

n = 8√3

so, m + n = 4√2 + 8√3 = 4(√2 + 2√3)

5. Determine the area

Answer

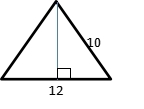
First step is determining the height using Pythagorean theorem.

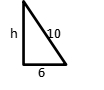
h = √(10² – 6²)

= √(100 – 36)

= √64

= 8

Then, determine the area

A = ½ x b x h

= ½ x 12 x 8

= 48

So, the area is 48.

6. Determine the ratio of area and perimeter

Answer

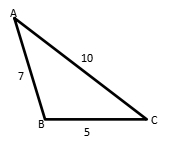
Area

It can be solved using Heron’s formula.

s = ½ x (7 + 5 + 10)

= ½ x 22

= 11

A = √(s(s-a)(s-b)(s-c))

= √(11 (11-7) (11-5) (11-10))

= √((11)(4)(6)(1))

= √264

= 16,25

Perimeter

P = 7 + 5 + 10 = 22

Ratio

A : P = 16,25 : 22

= 65 : 88

7. Determine the area and perimeter of triangle that has 4 cm and 6 cm as the sides and 60° as the angle between of them.

Answer

Illustrate the triangle

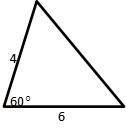
Area = ½ x m x n sinα

= ½ x 4 x 6 x sin60°

= ½ x 24 x ½ √3

= 6√3

Before determining perimeter, first step is determining the third side (let it as a) using cosines rule.

a^² = 4² + 6² – 2.4.6.cos60°

= 16 + 36 – 48. ½

= 28

a = √28

= 2√7

Then Perimeter = 2√7 + 4 + 6 = 10+2√7