Table of Contents
Definitions
Just an easy way to remember how Sine, Cosine and Tangent work:
Soh… (Sine = Opposite / Hypotenuse)
…cah… (Cosine = Adjacent / Hypotenuse)
…toa (Tangent = Opposite / Adjacent)
Right Triangle
Firstly, the names Opposite, Adjacent and Hypotenuse come from the right triangle:
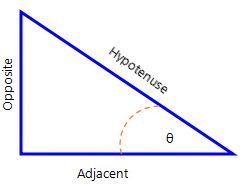
- “Opposite” is opposite to the angle θ
- “Adjacent” is adjacent (next to) to the angle θ
- “Hypotenuse” is the longest one
Sine, Cosine, & Tangent
Sine, Cosine, and Tangent are the 3 main functions in trigonometry.
They are often shortened to sin, cos and tan.
The calculation is simply one side of a right angled triangle divided by another side. we just have to know which sides, and that is where “sohcahtoa” helps.
For a triangle with an angle θ , the functions are calculated this way:
| Sine | soh… | sin(θ) = opposite / hypotenuse |
| Cosine | …cah… | cos(θ) = adjacent / hypotenuse |
| Tangent | …toa | tan(θ) = opposite / adjacent |
What are the sine, cosine and tangent of 60° ?
A 60° triangle has a hypotenuse (the longest side) of length 2, an opposite side of length √3 and an adjacent side of 1, like this:
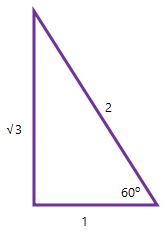
Now we know the lengths, we can calculate the functions:
| Sine | soh… | sin(60o) = √3/2 |
| Cosine | …cah… | cos(60o) = 1/2 |
| Tangent | …toa | tan(60o) = √3 |
