Rhombus: Definition, Properties, Area, Perimeter, Examples

by

What Is Rhombus

Geometry has some type of shape. Especially in plane geometry, one type of quadrilateral is rhombus. Specifically, rhombus is special type of parallelogram that has four sides that has same length.

It is like square, but the angles in rhombus need not be right angles. Beside that it is also has diagonals that each of them bisects two opposite interior angles.

Another name of rhombus is “rhomb” or “diamond”. It is identic with in playing card. Rhombus is also used in many things in real life.

For example, it is applied in kite, windows, earing etc.

Properties of Rhombus

There are some properties of rhombus:

  1. All of side has same length
  2. The opposite sides are parallel
  3. The opposite angles are same.
  4. The diagonals bisect each other. It makes right angle.
  5. The diagonal bisects two opposite angles.

Area of a Rhombus

The area of a rhombus is an area that is bordered by four same sides that has same length. There are some formula or the area to each type of rhombus.

  • Area is multiplication between height and the base.

A = height x base

A = h x b

Area of Rhombus
  • Area is a half of multiplication between first and second diagonal.

A = (D1 x D2) / 2

Area of Rhombus 2
  • Area is multiplication between base square and sin of any angle.

A = s x h

  = s x s.sinα

   =s2 x sinα

Area of Rhombus 3

Perimeter of a Rhombus

Perimeter means the sum all of rhombus’ sides. Let s as the length of side, then

Perimeter = 4 x s

Perimeter of Rhombus

Examples

  1. Given a rhombus KLMN that has LM = x+5, KL = 2x-9, then 2x = …?
Answer
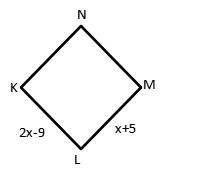
Rhombus Examples 1

Remember the properties that KL = LM.

Then,

2x – 9 = x + 5

2x – x = 5 + 9

        x = 14

so, the value of 2x = 2.14 = 28.

2. Determine the ratio between area and perimeter of the rhombus.

Rhombus Examples 2
Answer
  • Area = h x b

= 8 x 9

= 72 cm2

  • Perimeter = 4 x 9 = 36 cm
  • Ratio of area and perimeter = 72 : 36 = 2 : 1

3. Calculate the area.

a.

Rhombus Examples 3a
Answer

Calculating the area needs the height.

Using Pythagorean theorem, we get

h = √(172 – 82) = √(289 – 64) = √225 = 15

then the area is:

A = h x b = 15 x 17 = 255

b.

Rhombus Examples 3b
Answer

First step is determining the length of diagonals.

Using Pythagorean theorem,

Let shortest diagonal is 2 x 6 = 12 cm

Then calculating for m

m = √(102 – 62) = √(100 – 36) = √64 = 8

so, longest diagonal is 2 x m = 2 x 8 = 16.

Consequently,

A = (D1 x D2) / 2

= (12 x 16) / 2

= 96