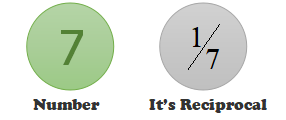
The reciprocal of a number is one divided by that number
Table of Contents
Reciprocal of a Fraction

To get the reciprocal of a fraction, simply switch the top and bottom of the fraction (numerator and denominator).
Reciprocal of a Reciprocal
The reciprocal of a reciprocal takes you back to where we started:

Remember that “Reciprocal” comes from the Latin reciprocus meaning returning.
Examples
| Number | Reciprocal | In Decimal | Reciprocal of Reciprocal |
| 2 | 1/2 | 0.5 | 2 |
| 4 | 1/4 | 0.25 | 4 |
| 10 | 1/10 | 0.1 | 10 |
| 1/2 | 2/1 | 2.0 | 1/2 |
| 1/4 | 4/1 | 4.0 | 1/4 |
| 1/10 | 10/1 | 10.0 | 1/10 |
| 2/3 | 3/2 | 1.5 | 2/3 |
| 3/4 | 4/3 | 1.33 | 3/4 |
| 5/6 | 6/5 | 1.2 | 5/6 |
Not for Zero
Every number except 0 has a reciprocal, because 1/0 is undefined
Reciprocal is what to multiply a value by to get 1
Try to multiply a number by its reciprocal:
5 × (1/5) = 5 x 0.2 = 1
Another example:
10 × (1/10) = 10 x 0.1 = 1
We always get 1
So:
Multiply a Number by Its Reciprocal Gets Us 1
The reciprocal is also called the “Multiplicative Inverse”
