Table of Contents
Definition of Pyramid
Pyramid is one of polyhedron form that connecting polygonal as the base and a point that called apex/vertex. As consequences there are base (polygonal that is like triangle, square, etc.) and some triangle sides as lateral sides.
Type of Pyramid Depends on the Base
Number of triangle depends on what type polygonal as the base. Besides that, one of types of pyramid depends on the base.
- Triangular pyramid
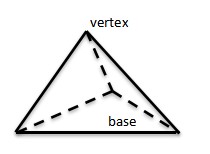
Triangular pyramid has one base (triangle), three lateral sides, and four points.
- Square pyramid
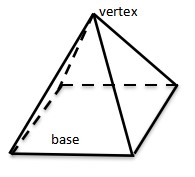
Square pyramid has a base (square), four lateral sides, and five points. This type is most popular than others because it is like pyramids in Egypt.
- Pentagonal pyramid
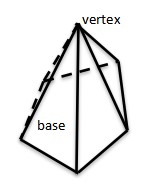
Pentagonal pyramid has a base (pentagonal), five lateral sides, and six points.
Based on the types of pyramids that depend on the base, there is keyword to determine number of lateral sides and the points based on the base.
If base is n-side then number of lateral sides is n and points is n+1
Type of Pyramid Depends on the Height
Types of pyramid are not only depending on the base but also the height. There are oblique and right pyramid.
- Oblique pyramid
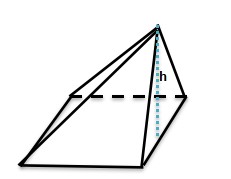
- Right pyramid
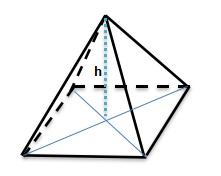
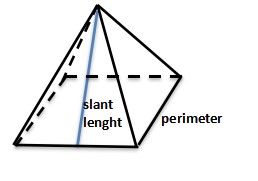
Surface area of a pyramid
Surface of the pyramid means the sum of all sides. They are base and all of lateral sides.
Surface area = base area + lateral area
But, if the base and laterals side are same,
surface area = base area + ½ x perimeter x slant length
Volume of a pyramid
Volume of a pyramid means the number of space in the pyramid. The formula is
V = 1/3.b.h
- b: area of the base
- h: height (it is measured from base to the vertex)
Examples of Pyramid’s Problems
1. Find the height of the pyramid that has base area = 9 cm and volume = 54 cm3!
Volume = ⅓.b.h
54 = ⅓.9.h
54 = 3h
h = 18 cm
2. A triangular pyramid has length of base = 6 cm. It is equilateral triangle. Height of pyramid = 8√3 cm. find the volume!
Because of the base is equilateral triangle, find the height first.
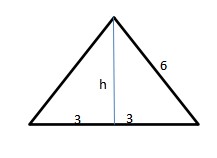
Height of base = √(62-32)
= √(36-9)
=√27
=3√3 cm
Base area = ½.base.height of base
= ½ .6.3√3
=9√3 cm2
Volume of pyramid = ⅓.base area.height
=⅓.9√3. 8√3
=72 cm3
3. Find the area all of square piramid’s surface if it has base area 64 cm2 and the height is 10 cm!
Because of base area is 64 and it is square pyramid, so the side is √64 = 8 cm.
And then look at the picture to make it easily.
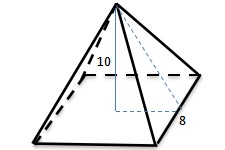
Focus on the blue lines. It is right triangle. Use Pythagorean’s theorem to find the height of lateral sides.
Height of lateral side = √(102+42)
=√(100+16)
=√116
=2√29 cm
Area of lateral side = ½ .8. 2√29
= 8√29 cm2
So, the area all of square pyramid = base area + lateral area
= 64 + 4.8√29
=64+32√29 cm2
