Table of Contents

Piecewise Functions Definition

A function can be expressed as a graph. But, not all of function has a whole graph. Some function has some pieces of the graph. It is called as piecewise function.

The pieces of a function depend on x value that input into the formula/function. In another words, it is possible that a function consists of more than or equals to two graphs.

General form of piecewise function is:

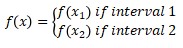
It is possible more than two f(x_n) and interval n^th.

There are piecewise functions:

1. The floor functions

It is special case of piecewise function. It is because floor function has infinite pieces.

2. The absolute value functions

It is the famous piecewise function. It has two type of x they are less than 0 (-x) and greater or equals to 0 (x).

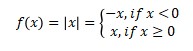
How to Solve Piecewise Function?

Piecewise function has two type of problem. First is determine the value of f(x) or y if it is known x. second is determine the function if it is known the graph. It will be explained one by one.

If it is known the graph

The problem is how to determine the function. The solution is taking any two points on the graph. Then using determine the linear equation formula, it will have the function as solution. Doing same way to determine other pieces of the graph.

Note: the formula is {(y – y₁) / (y₂ – y₁)} = {(x – x₁) / (x₂ – x₁)}

If it is known the function

The problem is how to determine the graph. The solution is same with how determine the graph in the general case.

Starting with first piece function and taking any point of x. it will easier if x=0 or other simple number.

After substitute to the function it will get the value of f(x) or y. take other sample point of x and y.

Next step is linking the point on the coordinate.

Paying attention on the boundary. Whether the point is including on the graph or not.

Note: sometimes there is continues or discontinues function. Continues function is drawing and linking the piecewise functions without picking up the pencil. But, discontinues function is drawing and linking the piecewise function by picking up the pencil.

Piecewise Functions Examples

Evaluate the given piecewise function at the given values of x.

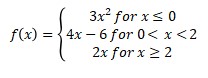
a. f(-1)

b. f(0,5)

c. f(2)

Answer

first, determine which one of the piecewise functions that has x = -1, which one for x = 0,5 and which one that has x = 2. They depend on the boundary/interval on each piecewise function.

a. f(-1) is on the first piecewise functions.

Then

f(x) = 3x²

f(-1) = 3(-1)² = 3

b. f(0,5) is on the second piecewise functions

then

f(x) = 4x – 6

f(0,5) = 4 (0,5) – 6 = -4

c. f(2) is on the third piecewise functions

then

f(x) = 2x

f(2) = 2(2) = 4

2. Graph the function and determine the domain and range.

Answer

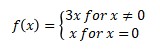
First step is taking any points as x and determine the value of f(x) or y. Remember how to read the first- and second-pieces function. First is f(x) = 3x and second is f(x) = x.
Second step is drawing and linking the point. Doing it by first piece and continued the second piece of function.

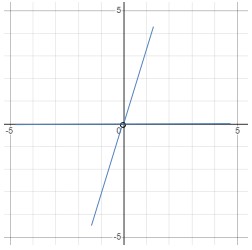
Because of the graph cover all of x value, the domain and the range is all of real numbers (-∞,∞).