Permutations and Combinations: Definition, Notation, Examples

Definitions

• a Combination is when the order doesn’t matter.
• a Permutation is When the order does matter.

In other words:

A Permutation is an ordered Combination.

Permutations

There are 2 types of permutation:

• Permutation with Repetition: such as the lock. It could be “444”.
• Permutation without Repetition: for example the first three people in a running race. You can’t be first and second.

Permutation with Repetition

The formula is written:

n^r

where,

• n is number of things to choose from
• r is number of things we choose of n
• repetition is allowed
• order matters

Permutation without Repetition

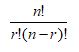
where,

• n is number of things to choose from
• r is number of things we choose of n
• repetition is NOT allowed
• order matters

Permutation Examples

1. For my account pin, there are 10 numbers to choose from (0,1,2,3,4,5,6,7,8,9) and we choose 6 of them. (You can choose same number twice or more)

n^r = 10 × 10 × 10 × 10 × 10 × 10 = 1,000,000

So there are 1,000,000 permutations for my pin.

2. What order could 7 runners be in top 3? (the runner in first place can’t be in second place)

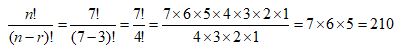
So there are 210 permutations for top 3 runners.

Permutation Notation

Instead of writing the whole formula, people use different notations such as these:

P(n,r) = ⁿP_r = _nP_r =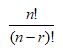

P(7,3) = 210

Combinations

There are 2 types of combinations (remember the order does not matter now):

• a combination with Repetition: such as coins in your pocket (5,5,10,10,10)
• a combination without Repetition: such as lottery numbers (5,14,17,22,30,34)

Combination with repetition

The formula is written:

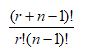
where,

• n is number of things to choose from
• r is number of things we choose of n
• repetition is allowed
• order doesn’t matters

Combination without repetition

The formula is written:

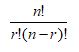
where,

• n is number of things to choose from
• r is number of things we choose of n
• repetition is NOT allowed
• order doesn’t matters

Combination Examples

1. There are strawberries, grapes, bananas, pineapples, and apples in refrigerator. I Want to make 3 cups of juice. How many combinations i can make? (repetition is allowed)

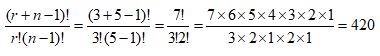
So, there are 420 combinations of juices i can make.

2. My teacher tell me to choose 3 girls from 7 girls in my class. How many choices i have? (repetition is not allowed)

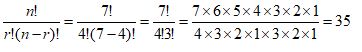
Combination Notation

Instead of writing the whole formula, people use different notations such as these:

C(n,r) = ⁿC_r = _nC_r =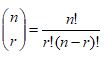

C(7,4) =35

Permutation & Combination Problems

1. Grace has 4 skirt, 5 t-shirt, 4 shoes. It can be combined each other. Determine how many ways she can combined skirt, t-shirt and the shoe.

2. Mr. Right’s family will take a photo together. He has two daughters and one son. He wants his child always stand between him and his wife. Determine how many positions to take photo.

3. There are 3 boys and 4 girls in a garden. They will watch a show and they sit in a bench. How many ways to arranged them if:

• There is no restriction
• Boys and girls alternate

4. There are 10 questions in mathematics’ test. Five questions must be done by students. Each student must answer 8 questions. How many ways to choose another five questions?

5. Sandy is sent to the store to get 5 different snacks of barbeque flavor and 4 different bottles of diet soda. If there are 10 different types of barbeque flavor, and 6 different types of diet soda to choose from, determine how many different Sandy’s choices.

6. There is a big group of students that consist of 7 men and 8 women. Teacher asked them to make a small group that consist of 5 students and at least 2 men in a group. Determine how many ways can it be done.