A series is the sum of the terms in a sequence (not the list of terms, like a sequence). The series with a finite number of terms is a easy to find the sum of the series just by adding the terms.
However, for the series with an infinite number of terms, the summation is more difficult and complicated. The series may or may not have a finite sum.
Table of Contents
Definition of Partial Sum
A Partial Sum is the sum of part of the sequence.
A Sequence is a set of things (usually numbers) that are in order.
This is the Sequence of even numbers from 4 onwards: {4, 8, 12, 16, 20 …}
The Partial Sum of the first 3 terms of sequence above is: 4+8+12 = 24
Partial sum of an infinite series is the sum of a finite number of consecutive terms beginning with the 1st term.
When working with infinite series, it is more helpful to examine the behavior of the partial sums.
Notation
Sigma (Σ)
Partial Sums are often written using Σ to mean “sum up”
So Σ means:
- Sum whatever is after the Sigma
- The values are shown below and above the Sigma
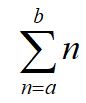
Where,
- So we sum n
- n goes from a to b
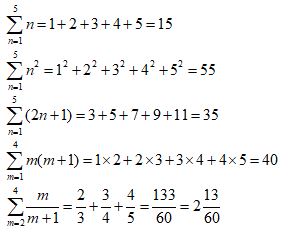
Partial Sums Properties
| Property | Example | Note | |
| Multiplying by a Constant | 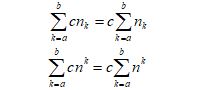 | 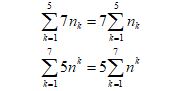 | nk could be k2, or k(k-7)+2, or anything c = constant value |
| Adding or Subtracting | 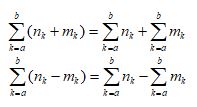 |  |
Partial Sums Shortcuts
Here are some shortcuts that make the sums a lot easier.
In each case we are trying to sum from 1 to value b.
| Shortcuts | Example | |
| Summing 1 equals b | ||
| Summing the constant c equals c times b | ||
| A shortcut when summing n | ||
| A shortcut when summing n2 | ||
| A shortcut when summing n3 |
