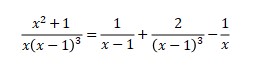Partial Fraction: Definition, Decomposition, Examples

by

What are partial fractions?

Fraction form can’t be ignored in mathematics. Some theorem or topics in mathematics using fraction and also partial fraction.

The fractions are possible to be split into two or more simple fraction and it is called partial fraction.  

Partial fraction is one of ways to calculate complex fraction to be easier. It is changed to be partial fraction first.

Partial fraction is also identic with polynomial. So, before calculating partial fraction, polynomial concept must be studied.

Partial fraction decomposition

Partial fraction decomposition means a process to “decompose” or start to simplify a fraction and taking it back apart. To decompose a fraction, first step is factoring the denominator.

As illustration, look at the fraction below.

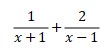
Partial Fraction

The fractions are simple fraction because it consists of two terms, but it can be more complex fraction if it is one term.

It will be

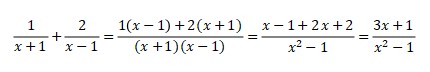
Partial Fraction 1

Now, how if the case is complex fraction?

Changing complex fraction to be partial fraction is the solution. One important thing in partial fraction is the degree of numerator is always less than the denominator.

There are steps to make partial fraction easily:

  1. Express it to be two terms with each denominator
  2. Look at the nominator. Multiply through by the bottom
  3. Find the constant by substituting the roots of the bottom

There many forms in denominator. Lok at the table. It shows the factor of denominator and the term in partial fraction

Partial Fraction Decomposition

Examples

1. Express to be partial fraction

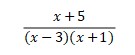
Example 1a

Answer:

  • Express it to be two terms with each denominator
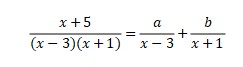
Example 1b
  • Look at the nominator. Multiply through by the bottom

x + 5 = a(x + 1) + b(x – 3)

  • Find the constant by substituting the roots of the bottom

First root

x – 3 = 0 → x = 3

Then

3 + 5 = a(3 + 1) + b(3 – 3)

8 = 4a

a = 2

Second root

x + 1 = 0 → x = -1

Then

(-1) + 5 = a(-1 + 1) + b(-1 – 3)

           4 = -4b

           b = -1

So, the answer is

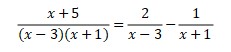
Example 1c

2. Express in partial fraction

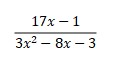
Example 2a

Answer:

Using step by steps

  • Express it to be two terms with each denominator
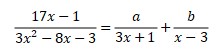
Example 2b
  • Look at the nominator. Multiply through by the bottom

17x – 1 = a(x – 3) + b(3x + 1)

  • Find the constant by substituting the roots of the bottom

First root

x – 3 = 0 → x = 3

Then

17(3) – 1 = a(3 – 3) + b(3(3) + 1)

           50 = 10b

             b = 5

Second root

3x + 1 = 0 → x = -⅓

Then

17(-⅓) – 1 = a((-⅓) – 3) + b(3(-⅓) + 1)

               a = 2

So, the answer is

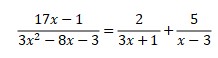
Example 2c

3. Express in partial fraction

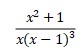
Example 3a

Answer:

This case is little different with previous examples. Based on the table (second row), it will be

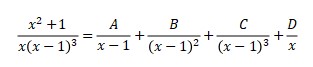
Example 3b

Look at the nominator. Multiply through by the bottom

x2 + 1 = Ax((x – 1)2) + Bx(x – 1) + Cx + D((x – 1)3)

Find the constant by substituting the roots of the bottom

First root x = 0 then

02 + 1 = A.0((0 – 1)2) + B.0(0 – 1) + C.0 + D((0 – 1)3)

        D = -1

Second root x = 1 then

12 + 1 = A.1((1 – 1)2) + B.1(1 – 1) + C.1 + D((1 – 1)3)

       C = 2

Then, how about A and B?

Pick any two other x-values, plug in, and get a system of equations so that A and B can be solved.

For example, x = 2 then

22 + 1 = A.2((2 – 1)2) + B.2(2 – 1) + C.2 + D((2 – 1)3)

  A + B = 1

Another x = -1, then

(-1)2 + 1 = A.(-1)(((-1) – 1)2) + B.(-1)((-1) – 1) + C.(-1) + D(((-1) – 1)3)

    2A – B = 2

Next, using the both of equation A dan B, eliminated them and will be get A = 1 and B = 0.

So, the answer is

Example 3