Parallelogram: Definition, Area, Perimeter, Diagonal, Types, Examples

by

Definition of Parallelogram

Parallelogram is a two-dimensional shape that has parallel sides each other. The parallel sides are equals in length. Parallelogram is also a quadrilateral because it has four sides.

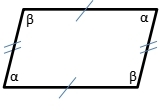
Definition of Parallelogram

The angles are same in the opposite. The sum of adjacent angles is 180° (supplementary angles).

Sum of α + β = 180°

Area of a Parallelogram

Parallelogram has height, base, and oblique sides. Area of parallelogram is area that is bordered by parallel sides.

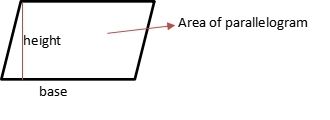
Area of Parallelogram

Area = height x base = h x b

Perimeter of a Parallelogram

Perimeter of parallelogram means sum of all sides of parallelogram.

Perimeter of Parallelogram

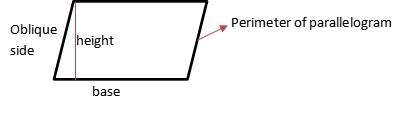
Parameter = P = base + base + oblique side + oblique side = 2 (b + o)

Diagonal of a Parallelogram

Parallelogram has two diagonals. They bisect each other. There are some consequences because of the diagonals of parallelogram.

Diagonal of Parallelogram
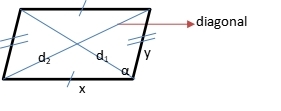
  • A diagonal of parallelogram divides the parallelogram to be two congruent triangles.
  • Two diagonals bisect each other in middle point.
  • Two diagonals divide parallelogram to be two (pairs) of congruent triangles.
  • Formula of any parallelogram is

d1 = √(x2 + y2 – 2xycosβ) = √(x2 + y2 + 2xycosα)

d2 = √(x2 + y2 – 2xycosα) = √(x2 + y2 + 2xycosβ)

Properties of a Parallelogram

  1. It has four sides
  2. The parallel sides (opposite sides) are same length and parallel.
  3. The opposites angles are equals.
  4. The sum of adjacent angles is 180°
  5. The diagonals bisect each other
  6. The diagonals divide parallelogram into two (pair) of congruent triangles.

Type of Parallelogram

There are some specific types of parallelogram. It depends on the length of the sides and the angles.

  1. Rectangle
  2. Square
  3. Rhombus

Examples

  1. Determine parameter of the parallelogram.
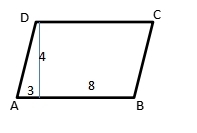
Parallelogram Examples 1
Answer

Look at the parallelogram. It needs to solve x first.

Using Pythagorean theorem to solve x.

x = √(42 + 32) = √(16+9) = √25 = 5 

then

Perimeter = 5 + (3+8) + 5 + (3+8) = 32

2. Determine area of the parallelogram

Answer

Area of parallelogram is multiplying of base and height. But there is not height yet.

Using Pythagorean theorem to determine the height.

h = √(102 – 62) = √(100-36) = √64 = 8

then

base = 18

Area = base x height = 18 x 8 = 144.

3. Determine the area and perimeter.

Answer

Look at the angle.

Because of total angle in triangle is 180° then the angles is 30°, 90°, and 60°.

Then the ratio is x, x√3, and 2x.

It is known that 6 = x.

So, x√3 = 6√3 and 2x = 12.

It can conclude that perimeter = 2 (20 + 12) = 2 (32) = 64 cm

And the area = 20 x 6 = 120 cm2.