Table of Contents
Definition of Parallel Lines
If 2 lines are parallel, their slopes are same.
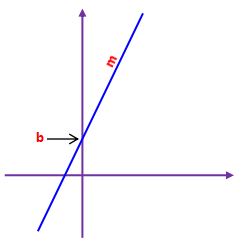
Slope is the value m in the equation of a line.
y = mx + b
If two lines are parallel lines, they will never intersect. They have exactly the same steepness which means their slopes are identical.
Find the equation of the line that is:
parallel to y = x
and passes though the point (7,4)
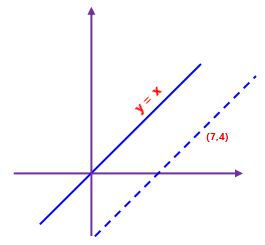
The slope of y= x is: 1
The parallel line needs to have the same slope of 1.
We can solve it using the “point-slope” equation of a line:
y − y1 = m(x − x1)
Put in the slope (1) and point (7,4):
y − 4 = 1(x − 7)
Put it in y = mx + b form:
y − 4 = x − 7
y = x − 3
*Note: this does not work for vertical lines
Since:
- Slope is a measure of the angle of a line from the horizontal
- Parallel lines must have the same angle
So:
Parallel lines have the same slope and lines with the same slope are parallel.
The only difference between the 2 lines is the y-intercept. If we shifted one line vertically toward the y-intercept of the other, they would become the same line. Parallel lines continue forever without touching.
Vertical Lines
The previous methods work nicely except for a vertical line.
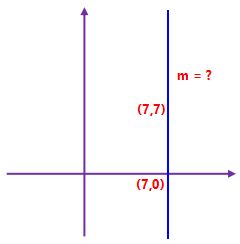
The gradient is undefined (as we cannot divide by 0):
m = (yA − yB) / (xA − xB)
m = (7 − 0) / (7 − 7)
m = 7/0 = undefined
So just rely on the fact that:
- a vertical line is parallel to another vertical line.
- a vertical line is perpendicular to a horizontal line (and vice versa).
Not The Same Line
They may be the same line (with different equation), and so are not parallel.
To find if they are really the same line, Check their y-intercepts (where they cross the y-axis) as well as their slope:
y = 2x + 1 and y − 1 = 2x
- For y = 2x + 1: the slope is 2, and y-intercept is 1
- For y − 1 = 2x: the slope is 2, and y-intercept is 1
They are the same line, so they are not parallel
Perpendicular Lines
Perpendicular lines do intersect, unlike parallel lines. Lines intersection forms a 90o or right angle.
2 lines are Perpendicular when they meet at a right angle (90°).
To find a perpendicular slope:
When a line has a slope of m, a perpendicular line has a slope of −1/m
In other words the negative reciprocal
Find the equation of the line that is
- perpendicular to y = x
- passes though the point (4, 4)
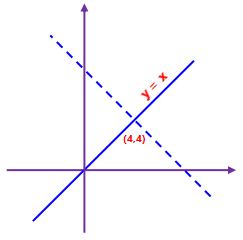
The slope of y= x is: 1
The negative reciprocal of that slope is:
m = −1/1 = −1
So the perpendicular line will have a slope of −1
y − y1 = −1(x − x1)
Put in the point (4,4):
y − 4 = (−1)(x − 4)
Put it in “y=mx+b” form:
y − 2 = −x + 4
y = −x + 2
Quick Check of Perpendicular
Perpendicular lines do not have the same slope. The slope of one line is the negative reciprocal of the slope of the other line.
The product of a number and its reciprocal is 1. If m1 and m2 are negative reciprocals of one another, they can be multiplied together to get -1.
m1 × m2 = -1
So to quickly check if 2 lines are perpendicular:
When we multiply their slopes, we get −1
y = 4x – 3 and y = -0.25x + 7
| Line | Slope |
| y = x | 4 |
| y = -x | -0.25 |
When we multiply the 2 slopes we get:
4 × (−0.25) = −1
We got −1, so they are perpendicular.
Summary
- parallel lines: same slope
- perpendicular lines: negative reciprocal slope (−1/m)
