Lines are parallel if they are always the same distance apart (called “equidistant“), and will never meet.
Table of Contents
Definition of Parallel Lines
Parallel lines in geometry are lines in a plane which do not meet. They don’t intersect each other at any point.
By extension, a line & a plane, or 2 planes, in 3D Euclidean space that do not share a point are said to be parallel.
However, 2 lines in 3D space which do not meet must be in a common plane to be considered parallel, if they aren’t in the common plane, they are called skew lines. Parallel planes are planes in the same 3D space that never meet.
The Use of Parallel Lines
Parallel lines are useful to find out the relationships between paths of objects & sides of various shapes.
For example, rectangles, squares, & parallelograms have sides across from each other that are parallel.
Think of parallel lines as a set of railroad tracks. The 2 rails of the track are created for the wheels on each side of the train to travel along.
Because the wheels of the train are always the same distance apart. Even when they turn, they do not get closer.
Parallel Lines Symbol
Parallel lines are indicated in formula with a pair of vertical pipes (||) between the line names, for example:
AC || BD
indicates that line AC is parallel to line BD.
Each line has many parallels. Any line that has the same slope as the original will never intersect with it.
Lines that would never cross, even if extended forever, are parallel.
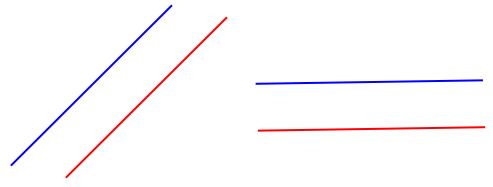
Graphing Parallel Lines
When 2 parallel lines are graphed, they must be at the same angle. So they’ll have the same slope or steepness.
Even though these 2 lines don’t start in the same point, you can see that they are equally slope. They decrease or slope downward at the same rate. So, they’re parallel.
Just remember
Parallel: Always the same distance apart and never touching.
Example
Parallel lines also point in the same direction.
They have so much in common. But, Parallel lines will never meet!
Pairs of Angles
When parallel lines get crossed by another line (which is called a Transversal), you can see that many angles are the same, as in this example:
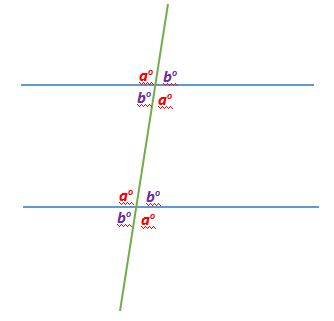
These angles can be made into pairs of angles which have special names.
Finding Parallel Lines
Those special pairs of angles can be used to find if lines really are parallel:
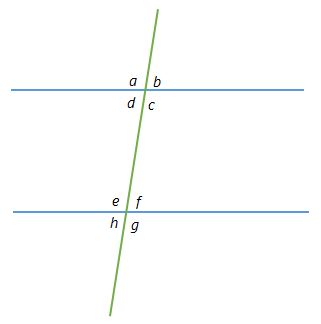
They are parallel lines if any pair of angle meet at least one of these conditions below.
| Condition | Example |
| Corresponding Angles are equal | a = e |
| Alternate Interior Angles are equal | d = f |
| Alternate Exterior Angles are equal | b = h |
| Consecutive Interior Angles add up to 180° | c = f |
