The line of symmetry is the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
Table of Contents
How to find a shape has a Line of Symmetry ?
- You can find a shape has a Line of Symmetry or not by folding it
- When the folded part sits perfectly on top (all edges matching), then the fold line is a Line of Symmetry.
Examples
| Plane Shape | Folding it | |
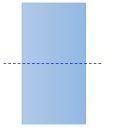 |  | The folding Line is Line of Symmetry |
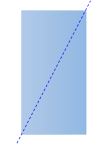 |  | The folding Line is NOT Line of Symmetry |
Triangle
A Triangle can has 3, or 1 or no lines of symmetry:
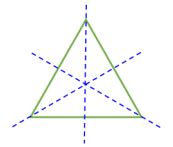 Equilateral Triangle (all sides equal, all angles equal) | 3 Lines of Symmetry |
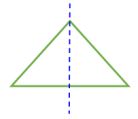 Isosceles Triangle (2 sides equal, 2 angles equal) | 1 Line of Symmetry |
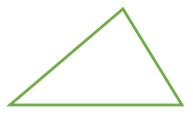 Scalene Triangle (no sides equal, no angles equal) | no Line of Symmetry |
Quadrilaterals
A Quadrilateral 4, 2, or 1 or no lines of symmetry:
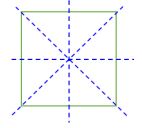 Square (all sides equal, all angles 90°) | 4 Lines of Symmetry |
 Rectangle (opposite sides equal, all angles 90°) | 2 Lines of Symmetry |
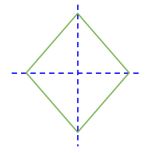 Rhombus (all sides equal length) | 2 Lines of Symmetry |
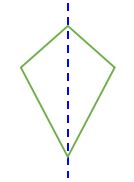 Kite | 1 Line of Symmetry |
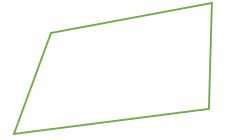 Irregular Quadrilateral | no Line of Symmetry |
Regular Polygons
| 3 Sides |  Equilateral Triangle | 3 Lines of Symmetry |
| 4 Sides |  Square | 4 Lines of Symmetry |
| 5 Sides | 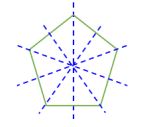 Regular Pentagon | 5 Lines of Symmetry |
| 6 Sides | 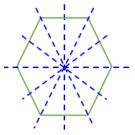 Regular Hexagon | 6 Lines of Symmetry |
| 7 Sides | 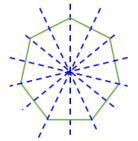 Regular Heptagon | 7 Lines of Symmetry |
| 8 Sides | 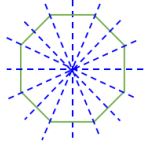 Regular Octagon | 8 Lines of Symmetry |
And the pattern continues:
A regular polygon with 9 sides has 9 Lines of Symmetry
A regular polygon with 10 sides has 10 Lines of Symmetry
…
A regular polygon with “n” sides has “n” Lines of Symmetry
Circle
Any line that goes through its center is a Line of Symmetry.
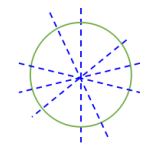
So a Circle has infinite Lines of Symmetry.
