A linear equation is an equation for a straight line. Equation of a line is one of algebra concept. It is basic concept of others. They are like in mathematics and physics. In real life, it is applied in speed calculation, cost of rental car / taxi, etc.
Table of Contents
General Form
Equation of a line has general form that is usually written as:
ax + by = c
(Standard form)
where a and b are coefficient of x and a is positive.
If there is 2x – y = -1 then the graph of equation of a line is
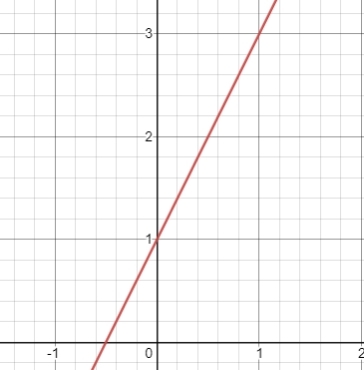
Pay attention on the graph.
Based on the graph, when x = 0 then y = 1 and when x = 1 then y = 3. It is appropriate with the equation of a line if it is substituted.
These are all linear equations:
y = 3x + 2
y = 5x + 7
y = 4x − 3
Different Forms
There are many ways of writing linear equations. They usually have constants (like “3” or “c”) and must have simple variables (like “x” or “y”).
These are linear equations
y = 2x − 5
Y/2 − 3 = 2(x + 4)
2y + 3x − 4 = 0
x = 5
y =7
The variables (like “x” or “y”) in Linear Equations do NOT have:
Exponents (like the 2 in x2)
Square roots, cube roots, etc
These are NOT linear equations:
Y3 − 5 = 0
√x − y = 7
X5/3 = 125
Slope-Intercept Form of The Equation of a Line
Slope (gradient) of a line is ratio between difference of y-axis and x-axis based on the two points in a line. It is also defined as ratio between vertical change over horizontal change. It is not always positive. Sometimes it is also negative sign. They are different in the direction of the slope.
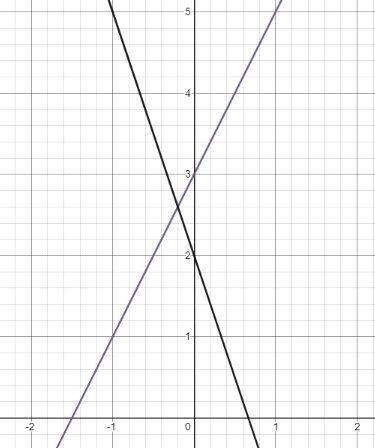
The blue line is positive slope and the black is negative slope.
Before talking about slop-intercept form of the equation of a line, there is special case between lines and slope/gradient. If there are two lines that has m1 and m2 as the gradient, then
- They are perpendicular
m1 x m2 = -1
They are negative reciprocal each other.
- They are parallel
m1 = m2
Another general form of equation of a line is slop-intercept form.
y = mx + c
Where:
- m : slope / gradient
- x : variable
- c : constant (y-intercept)
y = x
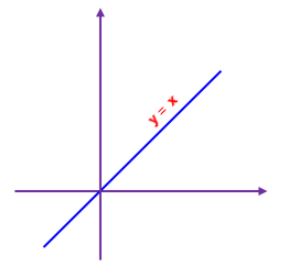
From the illustration above, we got
Slope: m = 1
Intercept: b = 0
If there is an equation y = 2x + 3, then the graph is
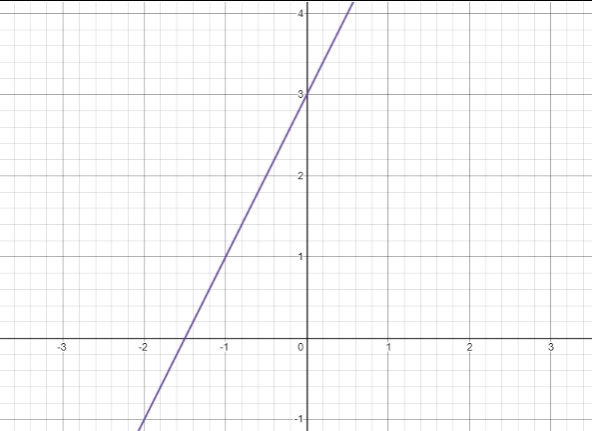
Based on the graph, the points are (0,3) and (-1,1).
Using the points, it can be determined the slope/gradient.
m = [y2 – y1] / [x2 – x1]
then
(0,3) as (x1, y1) and (-1,1) as (x2,y2)
m = [y2 – y1] / [x2 – x1]
= [1 – 3] / [-1 – 0]
= [-2] / [-1]
= 2
Point-Slope Form of the equation of a line
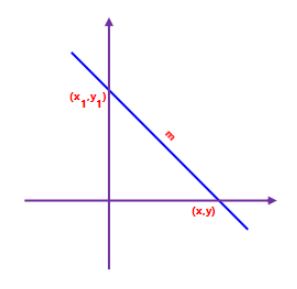
Point-slope form of the equation of a line is the method to determine equation of a line using slope/gradient. Besides that, it also uses a point in a line. The general form is
y – y1 = m (x – x1)
where:
(x,y) : variable in a line
(x1,y1) : one of point in the line
m : slope/gradient
y − y1 = m(x − x1)
y − 7 = 2(x − 4)
It is in the form y − y1 = m(x − x1) where:
y1 = 7
m = 2
x1 = 4
Examples
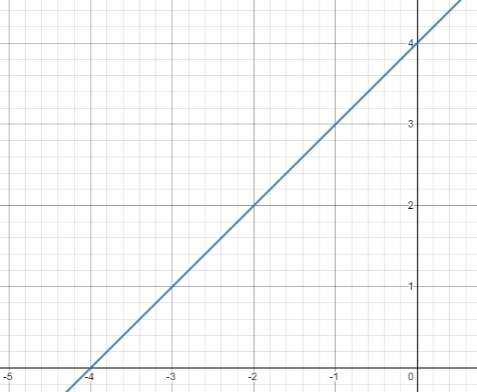
1. Write the equation of the graph
a.
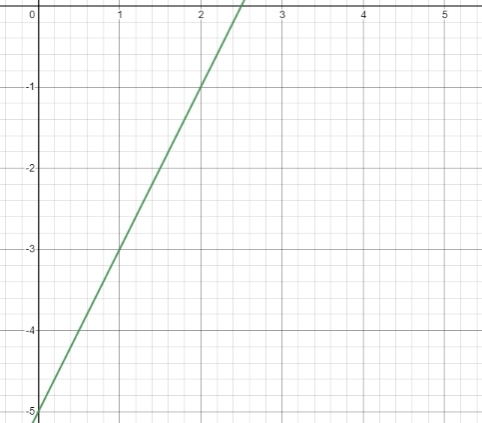
b.
a. Determine the gradient (m) first. It is trough (-4,0) and (0,4) then
m = [y2 – y1] / [x2– x1]
= [4 – 0] / [0 – (-4)]
= 4 / 4
= 1
Then the equation of the line is
y – y1 = m (x – x1) → use one of the points (0,4) or (-4,0). It use (0,4).
y – 4 = 1 (x – 0)
y = x + 4 or x – y = -4
it is also can be solved by using [y – y1] / [y2 – y1] = [x – x1] / [x2 – x1] and the points are (0,4) and (-4,0).
[y – y1] / [y2 – y1] = [x – x1] / [x2 – x1][y – 4] / [0 – 4] = [x – 0] / [-4 – 0]
[y – 4] / [-4] = x / [-4]
-4y +16 = -4x (divided by 4)
-y + 4 = -x
y = x+4 or x – y = -4
b. You can use one of the ways that is like point (a).
Determine the gradient (m) first. It trough (0,-5) and (1,-3) then
m = [y2 – y1] / [x2– x1]
= [-3 – (-5)] / [1 – 0]
= 2 / 1
= 2
Then the equation of the line is
y – y1 = m (x – x1) → use one of the points (0,-5) or (1,-3). It use (0,-5).
y – (-5) = 2 (x – 0)
y = 2x – 5 or 2x – y = 5
2. Determine the equation of a line if it has gradient -3 and it trough (1,2).
Using point-slope form of the equation of a line then
y – y1 = m (x – x1)
y – 2 = -3 (x – 1)
y – 2 = -3x + 3
y = -3x + 5
3. Determine the equation of a line if it has y-intercept is -1 and perpendicular to line x – y =
Let m1 as the gradient of x – y = 4. It is 1 because y =1.x – 4.
m2 as the gradient of the line in the question.
Then
- Perpendicular means
m1 x m2 = -1
1 x m2 = -1
m2 = -1
note: m1 and m2 are negative reciprocal each other.
- Y-intercept is -1. It means (0,-1).
- The equation of the line is
y – y1 = m (x – x1)
y – (-1) = -1 (x – 0)
y + 1 = -x
y = -x – 1 or x + y = -1
