Table of Contents
What is a Limit?
Limit means value of a function that approaches another value.
Limit is symbolized as
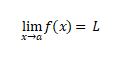
It is read as “limit of function of x, as x approaches to a equal to L”.
Look at the graph,
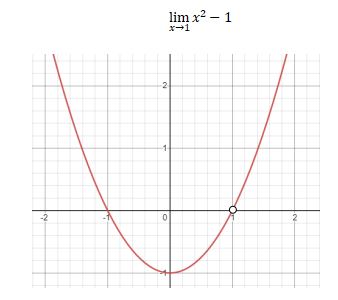
Properties of Limits
If there are two limits,
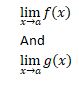
Then
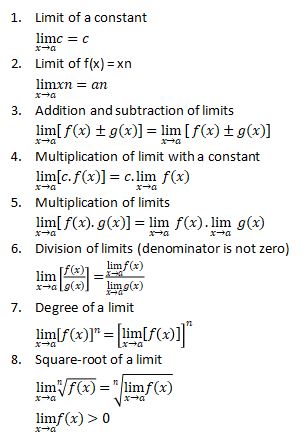
Limits to Infinity
limit to infinity is a special case. Infinity means there is no boundary of minimum and maximum value of infinity. It is symbolized as “∞”.
Remember concept of 1/∞. The result is none knows because it is undefined.
It is because there is no maximum and minimum value of infinity, so there is no maximum and minimum value of the answer. Maybe it can be -0,00… or 0,00…. It is just approaching a value but never same as the value.
How to determine the approaching value?
It uses limit’s concept.
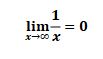
Remember that it does not means that the answer of 1/x is zero.
When x approaches to infinity (max or min value) then the answer is approaches to zero.
Evaluating Limits
Important concept in evaluating limits is the result cannot be 0/0. There are three concepts to evaluate limits’ problem:
1. Substitution
It is the first thing to do to evaluate or solve limits’ problem. If there is
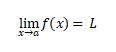
Then substitute the value of a to the function of f(x) to get L.
But if the answer is 0/0 then use other concepts to solve it.
2. Factorization
It is the second possibility concept to solve or evaluate limits’ problem. If the problem cannot be evaluated using substitution concept, then use factorization. Concept of this way is factoring the function of f(x). In another word, make it simplest form. Then use substitution concept to get the solution.
3. Conjugation
Conjugation method use to evaluate limits’ problem in fraction form [f(x)/g(x)] and it has square root form. The basic concept of conjugate is using the opposite sign of one of f(x) or g(x). it is also can be said that it uses opposite sign (+ or -) of one of numerator or denominator. If there is function (x+2)/(x+1) then it can use conjugate of numerator (x-2) or denominator (x-1). But it is also as fraction form and not change the value.
Another important thing in this concept is using concept of a2-b2 = (a+b)(a-b).
If there is limit’s problem
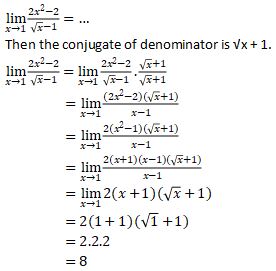
4. Infinity Limits
This method is used to solve infinity limits. The concept is paying attention to the degree of numerator and denominator. Numerator and denominator are divided by the biggest degree of them. There are simplest ways:
- If there is infinity limit
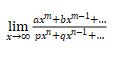
Then there are three possible answer.
1. If m = n then the answer is a/p
2. If m < n then the answer is 0
3. If m > n then the answer is ∞
- Specific problem of infinity limit
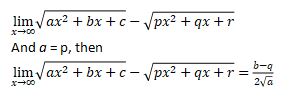
5. L’Hôpital’s Rule
It is used to make evaluating limit simple. It uses derivative concept. Sometimes it is not include as evaluating limit’s method because of some of students have not yet learn about derivative when they learn limits. This method is used if the result of the limit is 0/0 or ∞/∞.
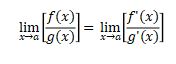
Learn about derivative topic to learn more about L’Hôpital’s rule (include: derivative of trigonometry).
Examples

