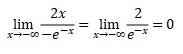L’hopital’s rule: Definition, Proof, Examples

What is l’hopital’s rule

L’hospital rule is one of ways to make limit easier to solve. It was introduced by French mathematicians, Guillaume de l’Hôpital.

It was 1969 in his book “Analyse des Infiniment Petits pour l’Intelligence des Lignes Courbes.”

L’hospital rule use derivative concept. In calculus, L’hospital use derivative to determine limit value in irregular form.

Aplying L’hospital concept changing irrgular form to be regular form then it will be easy to solve. L’hospital differentiate the numerator and denumerator. So, it can be wrote

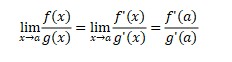
When to l’hopital’s rule

L’hospital rule is applied when a ^case/_poblems can not be solved by using common limit concept (subtitution method). It means the results are ⁰/₀ or ^±∞/_±∞.

So, in another words, first step to solve limit problem is subtitute the value that is approached by x. If it has ⁰/₀ and ^±∞/_±∞ then apply l’hospital rule.

If there is a case

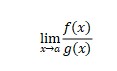
It will use L’hospital rule if:

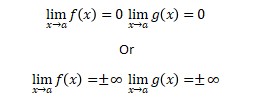
Beside that, there are other intermediate forms that can be solve with L’hospital rule:

0 x ∞, 1^∞, ∞ – ∞, ∞⁰

Note:

Usually, there is mistake if using L’hospital to solve limit problem by using derivative concept in fraction form. It is because L’hospital rule just differentiate numerator and denumerator without derivative rule in fraction form. The both of them will give different answer.  

l’hopital’s rule proof

There is proof or L’hospital rule that can be used to uderstand why it can be changed to be derivative.

Suppose that f(a) = g(a) = 0 and g(a) ≠ 0.

Then for any x, f(x) = f(x) – f(a) and g(x) = g(x) – g(a), then

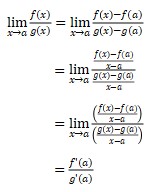
The definition,

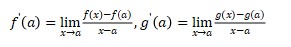
Since f’ and g’ are assumed to be continuous, f’(a)/g’(a) is also

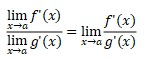
 It is proved that L’hospital rule changed limit problem to be derivative.

l’hopital’s rule examples

Find the value of

1.

Answer:

Using limit concept, it will be

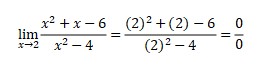
Because of the result is 0/0, it must use L’hospital concept. It will be

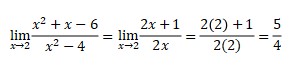
2.

Answer:

Using limit concept

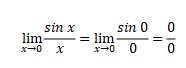
Because of the result is ⁰/₀, then

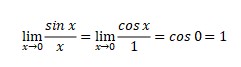
3.

Answer:

Using common concept of limit

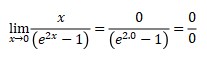
Using L’hospital concept

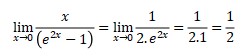
4.

Answer:

Using common concept of limit

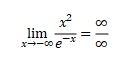
Using L’hospital concept

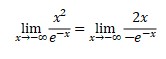
But it is still has answer ^∞/_∞. Applying second l’hospital rule