Table of Contents
Definition
Integration by Substitution (also called “The Reverse Chain Rule” or “u-Substitution” ) is a method to find an integral, but only when it can be set up in a special way.
It is an important method in mathematics. Integration by substitution is the counterpart to the chain rule for differentiation.
When it is possible to perform an apparently difficult piece of integration by first making a substitution, it has the effect of changing the variable & integrand.
For definite integrals, the limits of integration can also change. For this unit we’ll meet several examples. To master integration by substitution, you need a lot of practice & experience.
Note:
Sometimes an apparently sensible substitution doesn’t lead to an integral you will be able to evaluate. So, you need to try out alternative substitutions.
∫ f(g(x)) g′(x) dx = ∫ f(u) du, where u=g(x) and g′(x) dx = du
- When we can put an integral in this form:
∫ f(g(x)) g′(x) dx
- Then we can make g(x) = u and g′(x) dx = du
- Then integrate ∫ f(u) du
- And finish up by re-inserting g(x) where u is.
Examples
| f(x) dx | u | du | Substitution | Integral of ∫ f(u) du | Integral of ∫ f(x) dx |
| ∫ (x+1)3 dx | x+1 | 1 dx | ∫ u3 du | 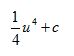 | |
| ∫ cos(x2) 2x dx | x2 | 2x dx | ∫ cos(u) du | sin u + c | sin x2 + c |
