Table of Contents
Definition of Inequalities
Inequalities is different with equality clearly. Equality use equal sign (=) but inequality use inequal sign (≠, >, <, ≤, ≥). Look at the table to understand about the inequality signs.
| Sign | Meaning | Example |
| ≠ | Not equals with … | 1 ≠ 2 |
| ≥ | Greater than or equal to … | a2+1 ≥ 10for a≥3or a≤-3or can be written as a = 3, 4, … or a = …, -4, -3 |
| ≤ | Less than or equal to … | x-2 ≤ 1for x = …, 1, 2, 3 or can be written as (x≤3) |
| > | Greater than .. | 2x > 4For x = 3, 4, 5, … |
| < | Less than … | x +1 < 2for x = …, -1, 0 |
Solving Inequalities
Solving inequality means determine the value of the variable (the solutions). In inequality problem, sometimes the solution consists of more than one value. There are steps to solve inequalities:
- Change the form to be “variable on the left side and other on the right side”
- Divide the right side with coefficient of the variable on the left side. It is like solving equation. But pay attention with the sign. Sometimes it has same sign but in other condition it has different sign (the opposite sign). There are some possibilities of the sign and the opposite:
| Sign | Opposite sign |
| ≥ | ≤ |
| ≤ | ≥ |
| > | < |
| < | > |
The sign can be changed if:
- Multiply or divide by negative number.
- Move from left side to the right side and vice versa.
But the inequality will have same sign if:
- Add or subtract with any numbers in both side
- Multiply or divide by positive number
- Simplify the inequalities
Some inequalities have interval solution. It can be written in more than one type. Look at the table.
| Inequality | Interval notation |
| x > a | (a,∞) |
| x < a | (-∞,a) |
| x ≥ a | [a, ∞) |
| x ≤ a | (-∞,a] |
| a ≤ x ≤ b | [a,b] |
| a < x < b | (a,b) |
| a ≤ x < b | [a,b) |
| a < x ≤ b | (a,b] |
Note:
- a,b are any numbers
- “[“ or “]” means the number include as solution.
- “(“ or “)” means the number is not solution
It is like equations that have some type (linear, quadratic, etc), inequalities have too. It will be explained about linear inequalities and quadratic inequalities.
Linear Inequalities
The differences of linear inequality and equation is the solution. It is because the sign of them is difference.
For example: 2x+1 > 0.
How to determine the solution?
Using step by step inequality concept, it will be:
2x+1 > 0
2x > -1 (move to the right side)
x > -½ (all of numbers that more than – ½ but it is not include as the solution)
How is the graph of 2x+1>0 ?
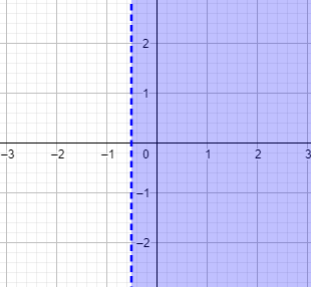
The blue area shows the solution. There are some numbers/values as the solution. But in – ½ it is not solution so it has dotted line.
Using number line, it will be

Blue area is solution. But, the number -½ is not solution, then it has empty point.
Quadratic Inequalities
Remember that quadratic equation is ax2+bx+c=0. But in quadratic inequalities, it is not “=” but inequality signs.
Quadratic inequalities have range number or more than one possible solution.
For example: x2 + 4 ≥ 8
How to solve it?
Using step by step inequality concept:
x2 + 4 ≥ 8
x2 ≥ 8 – 4
x2 ≥ 4
x = ±2 (it will easier if the sign changed to be equation in quadratic inequalities’ problem)
then use number line

substitute any number between of them, it will easier if let x = 0 then
x2 + 4 ≥ 8
02 + 4 ≥ 8 (false)
Then the right answer is less than -2 or more than 2. It can be written as x ≥ 2 or x ≤ -2.
Note:
- If you have more complex quadratic inequalities, factorize it and solve it as an equation. Then, determine the (interval) solution using line number.
- If the problem is fraction form, remember that the denominator is always not equals to zero.
How is the graph?
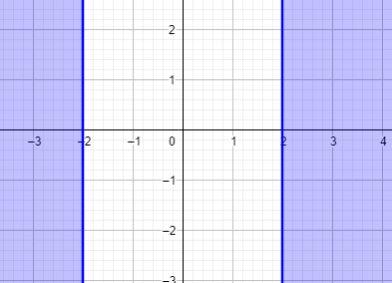
The blue area shows the solution. It has two solutions, there are x ≥ 2 or x ≤ -2.
Using number line, it will be:

Blue areas are solutions. They are x ≥ 2 or x ≤ -2.
Absolute value inequalities
Inequality means not equal. It possible be greater, less than, etc. It uses inequality signs (>, <, ≤, and ≥). Consequently, the solution of inequality is possible more than one number / solution. In another words, the solution can be an interval. Meanwhile, absolute value means nonnegative number or distance from origin regardless the direction. It is symbolized as |x| = x, read as absolute value of x is equal to x. Based on the definition, it is also mean that |-x| = x.
But, how about the definition of absolute value inequalities?
Absolute value inequalities mean nonnegative numbers that express absolute function with inequality sign. In spite of it has simple definition, but it has some rules to determine the solutions. Because of it is inequality sign, then it possible has more than one solution or has interval solution. The rules are:
If |a|≤ b, and b>0 then -b ≤ a ≤ b
If |a| < b, and b>0 then -b < a < b
If |a| ≥ b, and b>0 then a ≤ -b or a ≥ b
If |a| > b, and b>0 then a < -b or a > b
In other words, solving absolute value inequalities can be written as:
- Take a look at the rules. Determine which one of the rules that appropriate with the problem.
- Use algebra concept to subtract, add, or divide the side(s) to get the value of x (variable).
Example
1. Solve the inequalities.
a. 2(n+1)-4 > -2(n-2)
b. -6 ≤ 2(x-5) < 5
c. -1 < 2-3x ≤ 5
a. 2(n+1)-4 > -2(n-2)
2n+2-4 > -2n+4
2n-2 > -2n+4
4n > 6
n > 6/4
n > 3/2
b. -6 ≤ 2(x-5) < 5
-6 ≤ 2x-10 < 5
-6+10 ≤ 2x < 5+10
4≤ 2x <15 (divide by 2)
2 ≤ x < 15/4
Then, the solution is [2,15/4).
c. -1 < 2-3x ≤ 5
-1-2 < -3x ≤ 5-2
-3 < -3x ≤ 3
1 > x ≥ -1 (because of dividing by negative number)
Look at the interval. The solution is not (1, -1] but the solution is [-1,1).
2. Solve the inequalities.
a. x2+3x+2 > 0
b. x2-2(x-1) ≤ 37
c. {(x2-10)/(x+2)} + x-4 < x-3
a. x2+3x+2 > 0
(x+2) (x+1) = 0
x = -2 or x = -1
using line number

check: substitute x = 0 to the inequality and the result is right.
So, the answer is x < -2 or x > -1.
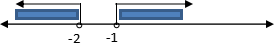
b. x2-2(x-1) ≤ 37
x2-2x+2 ≤ 37
x2-2x-35 ≤ 0
x2-2x-35 = 0
(x-7) (x+5) = 0
x = 7 or x = -5
using line number

the solution is [-5,7]
c. {(x2-10)/(x+2)} + x-4 < x-3
Be careful, it is fraction quadratic inequality.
(x+2) {(x2-10)/(x+2)} + x-4 < (x-3) (x+2) (to eliminate the denominator)
x2-10+(x-4)(x+2) < x2-x-6
x2-10+x2-2x-8 < x2-x-6
x2-x-12 < 0
(x-4) (x+3) = 0 (will be easier using equation sign)
x=4 or x=-3
using line number

then the solution is (-3,4) but because of denominator is x+2 consequently x≠-2.
3. |2x-1| ≤ 1
Based on the definition,
-1 ≤ 2x-1 ≤ 1
-1+1 ≤ 2x ≤ 1+1
0 ≤ 2x ≤ 2 (divide by 2)
0 ≤ x ≤ 1
Then the interval is [0,1].
4. |2x-4|>3
|2x-4|>3
Based on the definition of absolute value inequality,
| 2x – 4 < -3 2x < -3+ 4 2x < 1 x < ½ x < 0,5 | or | 2x – 4 > 3 2x > 3+4 2x > 7 x > 7/2 x > 3,5 |
Then the answer / interval is (-∞, ½ ) or (7/2 , ∞)
5. |x+1|<0
Because of absolute value is nonnegative number, then it has no solution. Because it is impossible if |x+1|<0. Based on the definition of absolute value is |x| = x and |-x| = x.
6. |-2+x|≥0
Because of absolute value is always positive numbers (nonnegative numbers), then x can be replaced by any real numbers. So, the answer is all of real numbers or it can be written as (-∞,∞).
7. |10+10x| – 6 < 4
Because of the question form is not same with the definition, then make it same first by adding +6 on the both sides.
|10+10x| – 6 + 6 < 4 + 6
|10+10x| < 10
The form is same as definition.
Next step: determine the value of x as the definition.
-10 < 10+10x < 10
-10 – 10 < 10x < 10 – 10
-20 < 10x < 0
-2 < x < 0
The solution is (-2,0).
