Some equations in x and y in mathematics do not explicitly define y as a function x and cannot be easily manipulated to solve for y in terms of x, even though such a function may exist.
If it happen, it is implied that there exists a function y = f( x) such that the given equation is satisfied.
The technique of implicit differentiation let you to find the derivative of y with respect to x without having to solve the given equation for y.
Implicit differentiation utilizes all of your basic derivative rules to find the derivative of equations that are not in standard form.
The chain rule must be used whenever the function y is being differentiated because of our assumption that y may be expressed as a function of x.
When you can’t solve for y, find the derivative
Table of Contents
Implicit vs Explicit
A function can be explicit or implicit:
Explicit:
- y = some function of x
- When we know x we can calculate y directly
Implicit:
- some function of y and x equals something else
- Knowing x does not lead directly to y
Example
In this form, y is expressed
as a function of x. In this form, the function is
expressed in terms of both y and x.
| Explicit Form | y = ± √ (r2 − x2), y is expressed as a function of x |
| Implicit Form | x2 + y2 = r2 , the function is expressed in terms of both y and x |
How to do Implicit Differentiation
- Differentiate with respect to x
- Collect all the dy/dx on one side
- Solve for dy/dx
x2 + y2 = r2
Differentiate with respect to x:
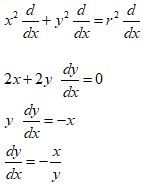
How to do Explicit Differentiation
Let’s also find the derivative using the explicit form of the equation.
To solve this explicitly:
- solve the equation for y
- differentiate
- substitute the equation for y again
Example:
x2 + y2 = r2
| 1 | solve the equation for y | x2 + y2 = r2 y2 = r2 – x2 y = ± √(r2 – x2) |
| 2 | differentiate y = + √(r2 – x2) | y = √(r2 – x2) = (r2 – x2)½ y ’= ½(r2 – x2)-½(-2x) y ’= –x(r2 – x2)-½ |
| differentiate y = – √(r2 – x2) | y = – √(r2 – x2) = – (r2 – x2)½ y ’=(-3/2)(r2 – x2)-½(-2x) y ’= 3x(r2 – x2)-½ | |
| 3 | substitute y = √(r2 – x2) to | y ’= –x / y |
| substitute y = – √(r2 – x2) to | y ’= 3x / (-y) y ’= – 3x / y |
Inverse Functions
Implicit differentiation can help us solve inverse functions.
The general pattern is:
- Start with the inverse equation in explicit form
- Rewrite it in non-inverse mode
- Differentiate this function with respect to x on both sides.
- As a final step we can try to simplify more by substituting the original equation.
| Step | Example |
| Start with the inverse equation in explicit form | y = sin−1(x) |
| Rewrite it in non-inverse mode | x = sin(y) |
| Differentiate | 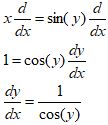 |
| simplify more | From the Pythagorean identity (sin2y + cos2y = 1), we get: cos y = √(1 − sin2 y ), so: By substitute x = sin y (from step 2), we get: |
Summary
To Implicitly derive a function (useful when a function can’t easily be solved for y)
- Differentiate with respect to x
- Collect all the dy/dx on one side
- Solve for dy/dx
To derive an inverse function
- Restate it without the inverse
- Use Implicit differentiation
