A Differential Equation is an equation with a function and one or more of its derivatives:
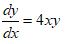
Example:
an equation with the function y and its derivative 
Homogeneous Differential Equations
A first order Differential Equation is Homogeneous when it can be in this form:
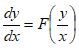
We can solve it using Separation of Variables but first we create a new variable 
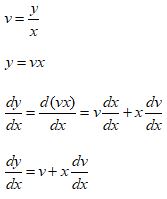
With 
we can solve the Differential Equation.
Example
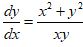
First, get it in 
form
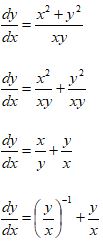
Now, we have a function of (y/x).
Then, substitute
We’ll get
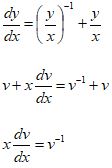
Now use Separation of Variables:
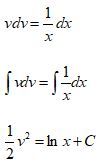
Put C in ln form with C = ln k
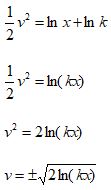
Now substitute back
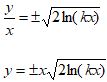
We got the solution.