Exponential Function: Definition, Equation, Graph, Properties, Inverse, Natural, Examples

What is an Exponential Function?

Exponential function is one of type of function. It is non algebraic (transcendental) function which cannot operate with addition, subtraction, multiplication, division of difference variables raised to some non-negative integer power.

Exponential function is not only in mathematics, but also in physics as the application.

Exponential Function Equation

The general form of exponential function equation is

f(x) = a^x

note:

• a is base. It is any real numbers that greater than 0.
• x is variable of the power (exponent). It is any real numbers.   
• exponential function has real numbers as the domain and positive real numbers as the range.

Exponential Function Graph

Graphing exponential function is like graphing other function. The steps are:

1. Make a list and determine the value of variable start from simple number (0,1,2,…).
2. Calculate the value of the exponential function by substituting the value into the function.
3. Draw the graph by using the point (coordinate)
4. Linking the points.

Properties of exponential function

There are properties of exponential function f(x) = a^x:

1. Graph of the function is always contain point (0,1). It is mean that if x = 0 then f(x) = a⁰ = 1.
2. For every number of a, it is always a^x ≥ 0.
3. The graph of a^x will decrease if 0 < a < 1.
4. The graph will increase if a^x > 1
5. If a^x = a^y then x = y.

Inverse

Exponential function has inverse. The inverse is logarithmic function.

f(x) = a^x then the inverse is log_a(x)

Besides that, sometimes it is also use natural logarithmic function (ln)

Natural Exponential Function

Exponential function is not only having general form equation, it is also specific form that is called natural exponential function.

f(x) = e^x

note:

e = 2.71828…

Exponential Function Examples

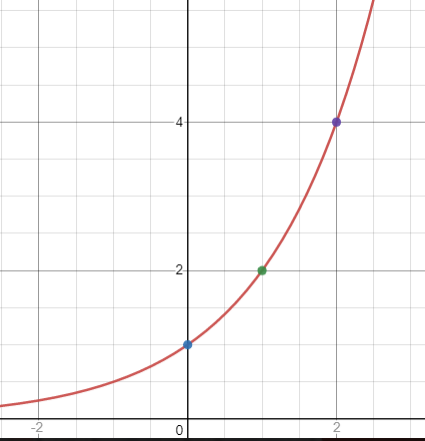
1. Sketch the graph of f(x) = 2^x.

Answer

Making list to determine the point (coordinate) of the graph.

X	f(x) = 2x	Coordinate
0	20 = 1	(0,1)
1	21 = 2	(1,2)
2	22 = 4	(2,4)
3	23 = 6	(3,6)
4	24 = 8	(4,8)

Then draw the graph appropriate with the point.

2. Solving each problems of exponential function

a. 3^2x = 3^1-3x

b. 7^1-x = 4^3x+1

c. e^4-7x + 11 = 20