Every function has each graph, but not all of the graph symmetric to x-axis, y-axis, or others. If the graph has symmetric, it concludes to specific case that the function is even or odd function.
Table of Contents
Even function and graph
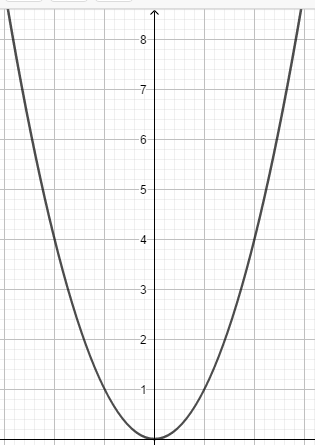
Even function is different mean with even numbers. The graph of even function is symmetric to y-axis. Look at the graph of y = x2. It is parabolic graph.
In mathematics, it can be written as
f(x) is even function if f(-x) = f(x) for every real numbers, xÎDf.
Odd function and graph
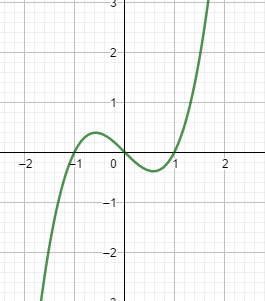
Odd function is different with even function. The graph of odd function is symmetric with point O(0,0). Look at the graph of y=x3-x.
In mathematics, it can be written as
f(x) is odd function if f(-x) = -f(x) for every real numbers, xÎDf.
Characteristics of even and odd function
There are some characteristics of even and odd function.
- Addition or subtraction between even function then the result is also even function
- Addition or subtraction between odd function then the result is also odd function
- Addition between odd and even function then the result is neither even nor odd function, except one of them is zero.
- Multiplication between even function then the result is even function.
- Multiplication between odd function then the result is even function.
- Multiplication between odd and even function then the result is odd function.
How to tell if a function is even or odd
A function is even or odd can be determine by substituting x value to be (-x). If it fulfills even or odd function concept, then it is. If x is changed to be (-x) and the result is equals to f(x) then it is even function. But if the result is equals to -f(x) is it odd function.
Neither Odd nor Even function
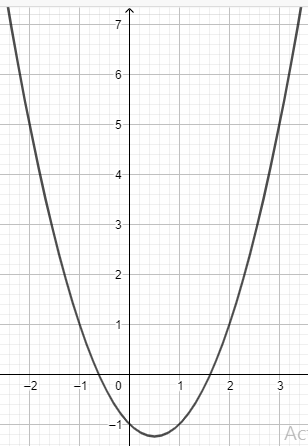
In spite of the topic talk about even and odd function, it does not mean that all of function can be categorized into the one of them. It is because there are also many functions that is neither even nor odd function. For example, if f(x) = x2 is even function, but f(x) = x2 – x – 1 is not. Look at the graph.
Examples
Determine whether the function is even or odd function
- f(x) = x4 – 2x2 + 3
f(-x) = (-x)4 – 2(-x)2 + 3
= x4 – 2x2 + 3
= f(x)
f(-x) = f(x)
then it is even function
2. g(x) = (x3 – 5x) / (x2 + 1)
g(-x) = ((-x)3 – 5(-x)) / ((-x)2 + 1))
= (-x3 + 5x) / (x2 + 1)
= – (x3 – 5x) / (x2 + 1)
g(-x) = – g(x)
then it is odd function.
3. k(x) = |x+3| – |x|
k(-x) = |(-x)+3| – |(-x)|
= |-x+3| – |-x|
≠ k (x)
≠ k(-x)
Then, it is neither odd nor even function.
4. f(x) = x4 – 2x2 + 3
g(x) = (x3 – 5x) / (x2 + 1)
determine (f)(x).g(x) whether even or odd function.
Based on the answer number 1 and 2, it is known that
f(x) = x4 – 2x2 + 3 is even function
g(x) = (x3 – 5x) / (x2 + 1) is odd function.
Then, based on the characteristics, the multiplying of even and odd function then the result is odd function.
