Determinant of a matrix is a scalar value. It is calculated from square matrix. Its means that only matrix that has dimension 2×2, 3×3, 4×4, etc. Determinant of matrix is used to solve some problem in mathematics.
They are like system of linear equation, calculus problem, and especially invers matrix. If there is matrix A, then determinant matrix A symbolized as “|A|”. Determinant of matrix uses simple arithmetic’s operation.
Table of Contents
Calculating Determinant of Matrix
Generally, there are two basic concept that used to calculate determinant of matrix. Beside that, it is rarely use more than 3×3 matrix to calculate the determinant.
Determinant of 2×2 Matrix
If there is matrix M2×2 and a, b, c, d are any numbers in the elements then
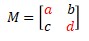
|M| = ad – bc
For example:
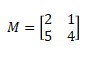
then
|M| = 2.4 – 5.1 = 8 – 5 = 3
Based on the concept and the example, the important things are the position of the elements and the ways (sign of operation).
Determinant of 3×3 Matrix
In spite of determinant of matrix has same basic concept but 3×3 matrix is little harder than 2×2 matrix. It needs carefulness.
There are two methods:
1. Minor – Cofactor method
- Take a simplest number in row or column.
- Determine the Minor based on the row or column (Mij).
- Determine cofactor (Aij).
- Find the determinant
- If there is matrix B3×3
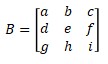
Then
Let the simplest row is first row, the elements are a1,1, a1,2, and a1,3. The numbers are a b c.
The minors are:
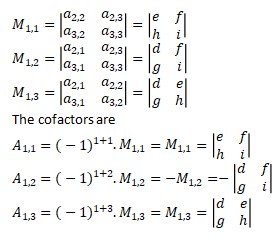
Then the final step is
|B| = a1,1 . A1,1 + a1,2 . A1,2 + a1,3 . A1,3
In another form,
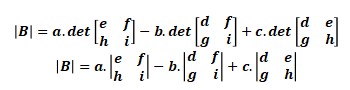
2. Sarrus Method
- Rewrite first and second column in the right side of matrix
- Make a line from top-left to bottom-right. Multiplying the elements and it has positive sign.
- Make a line from top-right to bottom-left. Multiplying the elements and it has negative sign.
If there is matrix B3×3
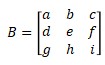
Then
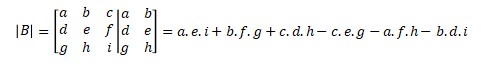
Example Determinant of Matrix
- Determine the determinant of matrix K.
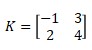
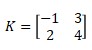
Then
|K| = ad – bc = (-1).4 – 2.3 = -4 – 6 = -10
2. Find the determinant of matrix 2A – 3B if
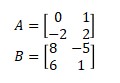
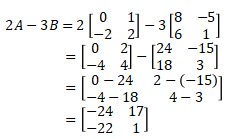
Then |2A – 3B| = (-24)(1) – (-22)(17) = -24 + 374 = 350
3. Determine the determinant of matrix Z if
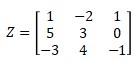
Use the easiest method based on your opinion.
Using minor – cofactor method
Take the last column as the simplest column

Determinant is
|Z| = a1,3 . A1,3 + a2,3 . A2,3 + a3,3 . A3,3
= 1 .29 + 0.2 + (-1).13
= 16
4. Determine the value of x2 if |H| = -18 and
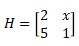
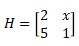
And |H| = -18
Then |H| = -18 = ad – bc
-18 = 2.1 – 5. x
-18 = 2 – 5x
5x = 20
x = 4
so, x2 = 42 = 16.
