Cube is a special case of a prism. There are many things in daily life that is cube. Some of them are Rubik, dice, ice cube, aquarium, etc.
Table of Contents
Definition of Cube
Cube is one of three-dimensional object. It has six squares as the sides (faces) so that it is also called hexahedron. Consequently, it has same measure of the length, width, and the height. Besides that, it also has eight vertices and twelve edges. All of the angle is right angle.
Properties of Cube
There are properties of cube:
- All of faces are square
- All of angle of a cube is right angle
- Vertices meet three edges and three faces
- Each face meets four other faces
- The face parallel with the opposite, and so does the edges.
- All of 12 diagonals of face of cube has same length
- All of four diagonals of cube has same length.
Surface Area of Cube
Surface area of a cube means total area that is covered the cube.
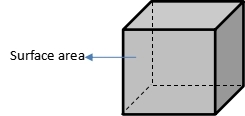
Because of cube consist of six squares, then the surface area is
Surface area = 6 x area of square = 6 x side x side = 6 x s2
Volume of Cube
Volume of cube means total space in the cube. Because of cube is three-dimensional object, it needs not only length and width in the base but also height.
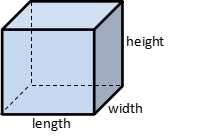
Volume = area of base x height
Square consist of six squares so that the base is square and the height is also side of square.
Volume of cube = side x side x side = s3
Diagonal of Cube
Cube is three-dimensional object, so that it has two kinds of diagonals.
- Diagonal of face
Diagonal of face is like diagonal of square. It is because all of the face of cube is square. A square has two diagonals, consequently a cube has 6 x 2 = 12 diagonals.
If there is a cube ABCDEFGH that length of the edge is a, then
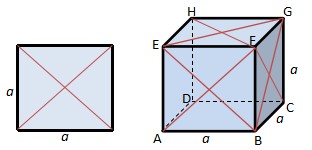
Diagonal of face = a√2
The diagonals are AF, EB, BG, CF, EG, HF, AH, DE, BD, AC, DG, HC.
- Diagonal of cube
Diagonal of cube means diagonal that link a vertex of cube with the opposite. There are four diagonals of cube.
If there is a cube ABCDEFGH that length of the side is a then
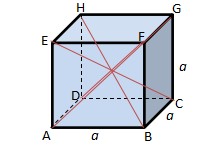
Diagonal of cube = a√3
The diagonals are AG, BH, CE, DF.
Examples
1. Determine the area of the shade area of cube.
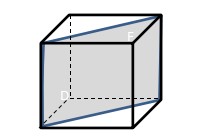
The shade area is called diagonal field. It is rectangle.
Focus on ∆ABC. It is right triangle so that use Pythagorean theorem to determine AC.
AC = √(52 + 52)
= √(25+25)
= √50
= 5√2
Then focus on the shade area ACGE. The length is 5√2 and the width is 5.
Area = l x w
= 5√2 x 5
= 25√2
2. Determine the surface area of a cube with the diagonal of cube is 3 cm.
Let a as the length of edge.
Diagonal of cube is = a√3 = 3 then a = √3.
Surface area = 6xs2
= 6 x a2
= 6 x (√3)2
= 6 x 3
= 18 cm2
3. Determine the volume of cube if the surface area is 36 cm2.
Let k as the length of edge, then
Surface area = 6 x s2
36 = 6 x k2
k2 = 6
k = √6
volume = s3
= (√6)3
= 6√6 cm3
