Angle is formed by two rays that have a common end point. There are some types of angle. Here they are.
Table of Contents
Type of Angle
In general, there are some kinds of angles:
1. Acute angle (less than 90°)
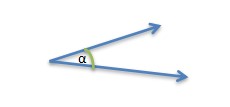
Learn more about acute angle.
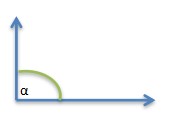
2. Right angle (90°)
3. Obtuse angle (more than 90° but less than 180°)
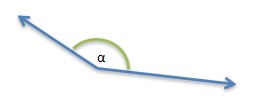
Learn more about obtuse angle.
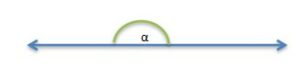
4. Straight angle (180°)
5. Reflect angle (more than 180°)
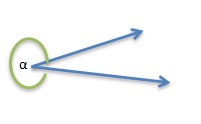
Learn more about reflect angle.
If two parallel lines are cut by another line (transversal) then there are angles that have same measure (same magnitude) which is called corresponding angles.
Corresponding Angels Theorem
Corresponding angles theorem says that
“If a transversal cuts two parallel lines, their corresponding angles are congruent”
Based on the theorem, there is eight angles that can be used to solve the angle’s problems
For more details, look at the picture.
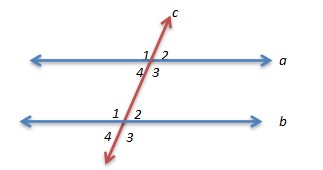
Based on the picture, lines a parallel with line b and they are cut by line c so there are angles that have same measure (same magnitude) which is called corresponding angles.
Based on the theorem, there are:
1. Alternate interior angles
Pair of alternate interior angles has same measure. Based on the picture, alternate interior angles are ∠a4 = ∠b2, and ∠a4 = ∠b2.
2. Alternate exterior angles
Pair of alternate exterior angles has same measure. Based on the picture, alternate interior angles are ∠a1 = ∠b3, and ∠a2 = ∠b4.
3. Consecutive interior angles
Sum of the pair of consecutive interior angles is 180°. They are ∠a4 + ∠b1 = 180° and ∠a3 + ∠b2 = 180°.
4. Consecutive exterior angles
Sum of the pair of consecutive exterior angles is 180°. They are ∠a1 + ∠b4 = 180° and ∠a2 + ∠b3 = 180°.
5. Corresponding angles
Pair of corresponding angles has same measure. Based on the picture, they are ∠a1 = ∠b1, ∠a2 = ∠b2, ∠a3 = ∠b3, and ∠a4 = ∠b4.
6. Vertical angles
Pair of vertical angles has same measure. Based on the picture, they are ∠a1 = ∠a3, ∠a2 = ∠a4, ∠b1 = ∠b3, and ∠b2 = ∠b4. It is also called ∠a1 is opposite of ∠a3.
Corresponding Angles Examples
- Find the a, b, and c!
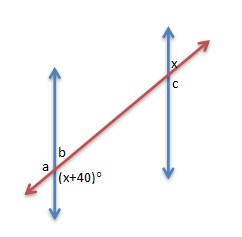
Using corresponding angles theorem,
- ∠x has same measure with angles in the opposite, so it is x (vertical angles).
- ∠x (based on the previously reason) and ∠(x+40)° are consecutive interior angles so the sum is 180°.
x + 40o + x = 180o
2x + 40o = 180o
2x = 140o
x = 70o
- ∠a is opposite of ∠(x+40)° so it has same measure, ∠a = 70o + 40o = 110o
- The sum of ∠b and ∠a is 180°. It is because they are supplementary angles.
Besides that, ∠b can be found by using reason that ∠b is supplementary with ∠(x+40)° so the sum is 180°, or using reason that ∠b and ∠x are alternate interior angles so they have same measure.
2. Find the x!
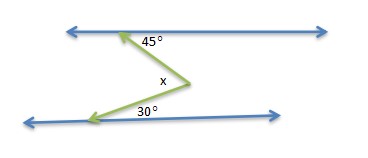
Making another line between the two parallel lines in the picture make it solve easily. Called it line a, b, and c.
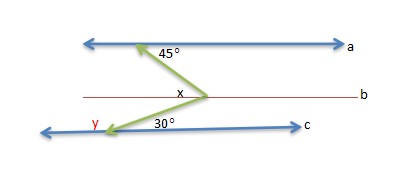
- Because of ∠y is supplementary angle with ∠30° so ∠y = 150° (we assume that there is ∠y)
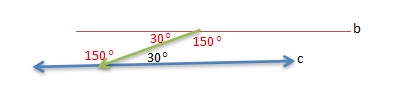
- Focus on lines b and c, so we have :
(Using alternate interior angles and consecutive interior angles)
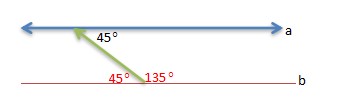
- Focus on lines a and b (Using consecutive interior angles)
- Now, look on the x. it is sum of angles on the top and bottom of line b.
x = 45o + 30o = 75o
3. The values of two corresponding angles are given to be p – 15° and 3p – 5°. Determine the magnitude of each corresponding angle.
First, determine the angle of p.
Corresponding angle means sum of them is 180°
p – 15° + 3p – 5° = 180°
4p – 20° = 180°
4p = 200°
p = 50°
Then, the magnitude of each corresponding angles are:
- p – 15° = 50° – 15° = 35°
- 3p – 5 = 3 (50°) – 5° = 145°.
4. Look at diagram.
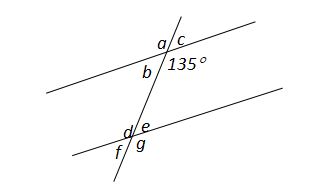
Determine the angle of b + 2d – e.
- The known angle is 135°, let it as x.
Then b + x = 180° (supplementary angle)
b + 135° = 180°
b = 45°
- Sum of b and d is 180° (consecutive interior angle)
b + d = 180°
45° + d = 180°
d = 135° (alternate interior angle with x)
- e is supplementary with d. It is also alternate interior angle. Consequently e = b = 45°.
- So, b + 2d – e = 45° + 2(135°) – 45° = 270°.
5. There are two lines, m and n. They are parallel. They are cut by a straight line named k. If the smallest angle is 2x+10 and the biggest one is 11x-25. Determine the value of x.
Based on the problem, the diagram of the lines is
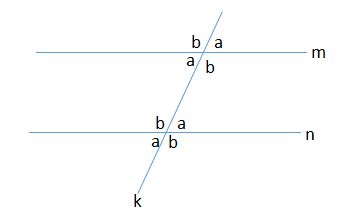
There is only two kind of angle. Let “a” as smallest angle and “b” as biggest angle. Why? Remember about corresponding angles.
a = 2x+10
b = 11x-25
a + b = 180°(supplementary angle)
then
2x + 10 + 11x – 25 = 180°
13x – 15 = 180°
13x = 195°
x = 15°
so, the value of x is 15°.
6. Look at the shape
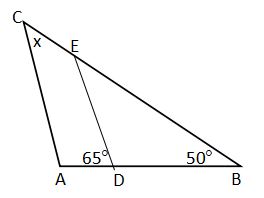
If AC//DE, determine x.
First step is focus on ÐEDB. It is supplementary angle of ÐADE, then it is 180° – 65° = 115°.
Next, focus on ∆DBE. Because of ÐDBE = 50°, ÐEDB = 115°, and sum of angle in triangle is 180°, then the ÐDEB = 180° – 50° – 115° = 15°.
It has been known that AC//DE. There is a line BC trough them. So, ÐACE = x is same with ÐDEB = 15° (corresponding angle).
The angle of x is 15°.
7. Look at figure. Determine the angle k if k = 2m – n and determine the relation of them (m,n,k).
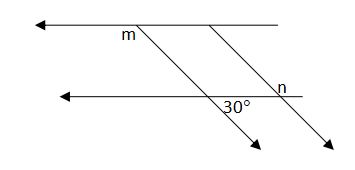
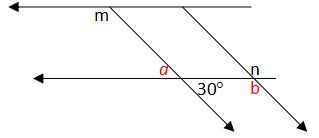
It will be easier if each (or some) of angle has a name.
Let a as the opposite angle of 30°, then a = 30°.
Let b is consecutive interior angle of 30°, then b = 180° – 30° = 150°
Consequently, m is consecutive interior angle of a, then m = 180° – 30° = 150°.
n is opposite angle of b, then n = b = 150°.
So, the angle of k = 2m – n = 2(150°) – 150° = 150°.
The relation between of three of them are have same measure (angle).
