Table of Contents
Definition of Continuous Function
Function describe as a relation of each value from the first set that is associated exactly one value from another set. Function has many types in mathematics. One of them is continuous function.
Continuous function is one of topics in calculus. Continue means unbroken. Continuous function is a function that has unbroken graph or there is not hole in the graph.
In another words, if there is a graph without a hole or breaks in an interval, it is called continuous function. Continuous function has important role in mathematics.
It is because it is the foundation before start to learn limit and derivative. Look at the pictures. Analyze whether it continuous function or not.
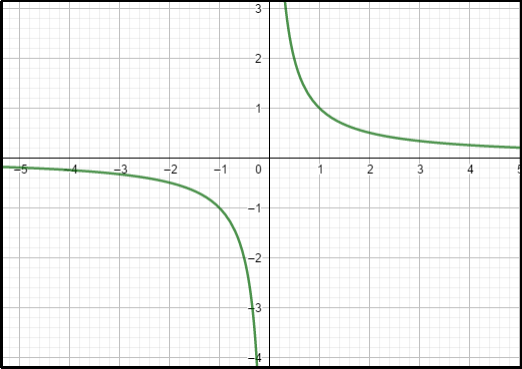
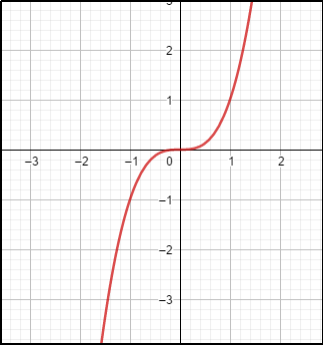
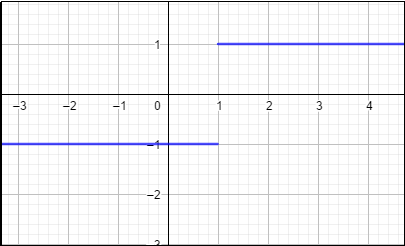
Based on the pictures, there is only b that is continuous function.
Making the graph is one of easy way to know whether the function continuous or not. But, because of not all of function can be drawn easily, it is important to know mathematical definition of continuous function.
Function f(x) is continuous function at point x = a, if there exist (a), (b), and satisfy (c).
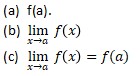
Function f(x) continue in interval (a,b) if only if f(x) continue in every point in the interval.
Continuous Function Examples
- Is the function continuous for all of xÎR?
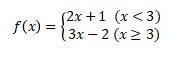
Answer:
Let us check one by one:
a. f(3) = 3(3) – 2
= 9 – 2
= 7 , f(3) exist
b. Check the limit. Remember, what must be satisfied by a function that has a limit.
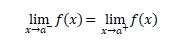
So, based on the problem:
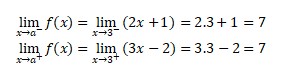
Because of the calculation above, the limit is exist.
Based on (a) and (b) so there is
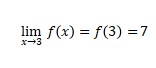
And it is concluded that the function continuous at x = 3.
2. Is the function continuous for all of x∈R?
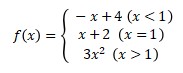
Answer:
a. Check the existence
f(x) = x + 2
f(1) = 1 + 2
= 3, f(1) exist
b. Check the limit
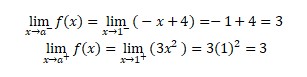
Because of the calculation above, the limit is exist.
Based on (a) and (b) so there is
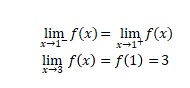
It is concluded that the function continuous at x = 1.
3. Is the function continuous for all of x∈R?
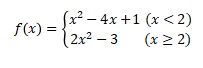
Answer:
a. Check the existence
f(x) = 2x2 – 3
f(2) = 2.22 – 3
= 8 – 3
= 5, f(2) exist
b. Check the limit
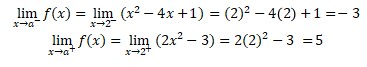
Because of the calculation above, the limit not exist.
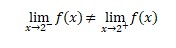
It is concluded that the function is not continuous at x = 2.
