Definitions
When two lines are crossed by another line (Transversal), Consecutive Interior Angles are the pairs of angles on one side of the transversal, but inside the two lines.
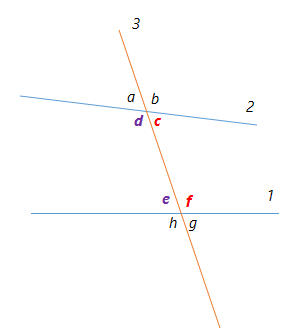
In this example, these are Consecutive Interior Angles:
(c and f) and (d and e)
The 2 angles in purple (d and e) make one pair of consecutive interior angles, and the other 2 angles in red (c and f) make another pair of consecutive interior angles. Both pairs are between the 2 lines and are both on the same side of the transversal.
Transversal is the line crossing the other two lines.
Identifying Consecutive Interior Angles
How to identify angles that are consecutive interior angles? The problem will ask you which other angle is the consecutive interior angle to a particular angle. For example:
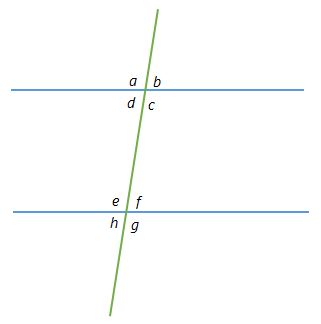
Question 1. Which other angle is the consecutive interior angle to a angle d ?
Look at the picture and choose the other angle that matches up with the angle in question.
In this example, the angle that pairs with angle d is angle e, because they are on the same side of the transversal and also between the 2 lines.
Question 2. Which other angle is the consecutive interior angle to a angle b ?
Look at the picture and find that angle b is outside the 2 lines. There is no consecutive interior angle to angle b because angle b itself is not part of a pair.
When the two lines are parallel, any pair of Consecutive Interior Angles add to 180o (supplementary).
Proof
Given: 1 ∥ 2 , and 3 is a transversal
Prove: m∠c + m∠f = m∠d + m∠e =180o
| Step | Statement | Reason |
| 1 | 1 ∥ 2 , and 3 is a transversal | Given |
| 2 | ∠c and ∠b form a linear pair ∠d and ∠a form a linear pair | Definition of linear pair |
| 3 | m∠c + m∠b =180o m∠d + m∠a =180o | Supplement Postulate |
| 4 | ∠b = ∠ f ∠ a = ∠e | Corresponding Angles Theorem |
| 5 | m∠c + m∠f =180o m∠d + m∠e =180o | Substitution Property |
