Triangles are congruent when all corresponding sides & interior angles are congruent. The triangles will have the same size & shape, but 1 may be a mirror image of the other.
2 triangles are congruent if they have:
- exactly the same three sides and
- exactly the same three angles.
We don’t have to know all 3 sides and all 3 angles, usually 3 out of the 6 is enough.
There are 4 ways to find if two triangles are congruent. Read the explanation below.
Table of Contents
How to Tell If Triangles are Congruent
Any triangle is defined by 6 measures (3 angles and 3 sides). But, to show that 2 triangles are congruent you don’t need to know all of them. Three of them in Various groups will do. Triangles are congruent if:
| 3 Measures | Detail |
| SSS (side side side) | All 3 corresponding sides are equal in length |
| SAS (side angle side) | A pair of corresponding sides & the included angle are equal |
| ASA (angle side angle) | A pair of corresponding angles and the included side are equal |
| AAS (angle angle side) | A pair of corresponding angles and a non-included side are equal |
SSS (side, side, side)
SSS stands for “side, side, side” and means that we have 2 triangles with all three sides equal.
For example:
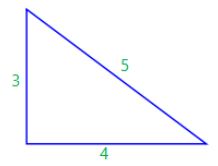
is congruent to:
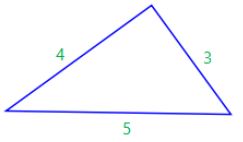
If 3 sides of one triangle are equal to 3 sides of another triangle, the triangles are congruent.
SAS (side, angle, side)
SAS stands for “side, angle, side” and means that we have 2 triangles where we know 2 sides and the included angle are equal.
For example:
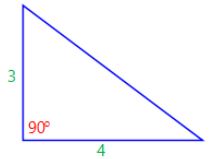
is congruent to:
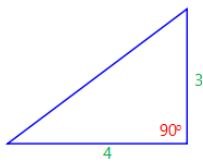
If 2 sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, the triangles are congruent.
ASA (angle, side, angle)
ASA stands for “angle, side, angle” and means that we have 2 triangles where we know 2 angles and the included side are equal.
For example:
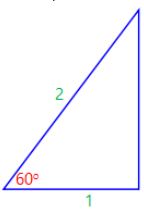
is congruent to:
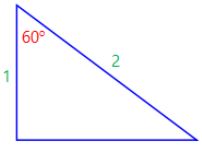
If 2 angles and the included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.
AAS (angle, angle, side)
AAS stands for “angle, angle, side” and means that we have 2 triangles where we know 2 angles and the non-included side are equal.
For example:
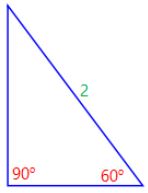
is congruent to:
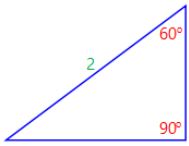
If 2 angles and the non-included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.
Can we use “AAA” ?
AAA “angle, angle, angle” means we are given all three angles of a triangle, but no sides.
This is NOT enough information to decide if 2 triangles are congruent!
Because the triangles can have the same angles but be different sizes:
Without knowing at least one side, we can’t be sure if two triangles are congruent.
Constructions
If you are asked to construct a unique triangle given what you know, for example: If you were given the lengths of 2 angles and the included side (ASA), there is only 1 possible triangle you could draw. If you drew 2 of them, they would be the same size & shape (the definition of congruent).
Properties of Congruent Triangles
If 2 triangles are congruent, then each part of the triangle (angle or side) is congruent to the corresponding part in the other triangle. Once you have proved 2 triangles are congruent, you can find the sides or angles of 1 of them from the other.
Use the acronym CPCTC to remember this important idea, which stands for “Corresponding Parts of Congruent Triangles are Congruent”.
In addition to angles & sides, all other properties of the triangle are the same too, such as perimeter, area, location of centers, circles etc.
