In geometry, 2 figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
Table of Contents
Definitions of Congruent Angles
Angles are congruent if they have the same angle measure in degrees. They can be at any orientation on the plane.
In case of angles, “congruent” is similar to saying “equals”. You could say “the measure of angle A is equal to the measure of angle B”. But in geometry, the correct way to say it is “angles A and B are congruent”.
Congruent Angles are 2 (or more) angles that have the same angle (in degrees or radians).
To be congruent, the angles measure must be the same, the length of the two arms making up the angle is irrelevant.
Examples
These angles are congruent.
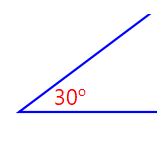 | 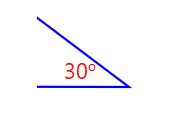 | 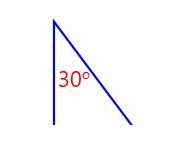 | These 3 angles are congruent because they have 30o (same angle) |
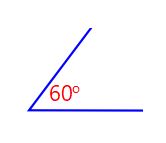 | 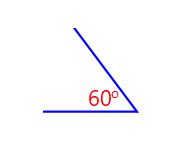 | 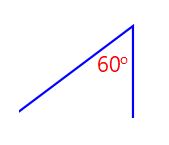 | These 3 angles are congruent because they have 60o (same angle) |
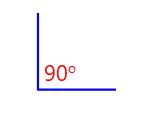 | 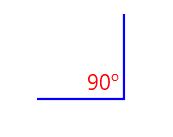 | 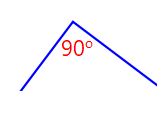 | These 3 angles are congruent because they have 90o (same angle) |
- They don’t have to point in the same direction.
- They don’t have to be on similar sized lines.
- Just the same angle.
The length of the angles’ edges or the direction of the angles has no effect on their congruency.
As long as their measure is equal, the angles are considered congruent.
Symbols of Congruence
The symbol for congruence is ≅
Also recall that the symbol for an angle is ∠, so the statement
∠ABC ≅ ∠DEF
is read as “The angle ABC is congruent to the angle DEF”.
