Table of Contents
Imaginary number
Imaginary number (when squared give a negative result)
i is the unit of imaginary number which is square root of -1
i = √-1, because i2=-1
So, (7i)2 = -7
Definition of Complex Number
A Complex Number is a combination of a Real Number and an Imaginary Number
4 + 7i, where 4 is Real Number, and 7i is Imaginary Number
Either Part Can Be Zero
- a Complex Number has a real part and an imaginary part.
- Either part can be 0
So,
- all Real Numbers are Complex numbers
- all Imaginary Numbers are Complex Numbers.
| Real Part | Imaginary Part | Complex Number | |
| Combination | 4 | 7i | 4 + 7i |
| Pure Real | 4 | 0i | 4 |
| Pure Imaginary | 0 | 7i | 7i |
We often use z for a complex number. And Re() for the real part and Im() for the imaginary part, like this:
z = a + bi, where Re(z) = a, Im(z) = b
Adding 2 complex numbers
To add 2 complex numbers, add each part separately
(a+bi) + (c+di) = (a+c) + (b+d)i
Multiplying 2 complex numbers
To multiply 2 complex numbers, each part of the first complex number gets multiplied by
each part of the second complex number
(a+bi)(c+di) = ac + adi + bci + bdi2
Because i2 = -1, so
(a+bi)(c+di) = ac – bd + adi + bci
Dividing 2 complex numbers
To divide 2 complex numbers, multiply both top and bottom by the conjugate of the bottom.
Note: A conjugate is where we change the sign in the middle
| Complex number | conjugate | Multiplying By the Conjugate |
| a + bi | a – bi | a2 + b2 |
| a – bi | a + bi | a2 + b2 |
So, to divide a + bi by c – di:
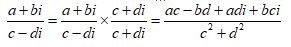
Or, to divide a + bi by c + di:
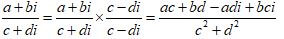
| Application | Result | |
| z1 | Given Re(z1) = 4, Im(z2)=7 | 4+7i |
| z2 | Given Re(z1) = 4, Im(z2)=-7 | 4-7i |
| z1+z2 | (4+4) + (7-7)i | 8 + 0i = 8 |
| z1 x z2 | 4×4 – 7x(-7) + 4x(-7)i + 4x7i | 44 + 0i = 44 |
| z1 / z2 |
