Derivative of a function of a real variable measures the sensitivity to change of the function value (output) with respect to a change in its argument (input).
Derivatives are a fundamental tool of calculus. The derivative of a function of a single variable at a chosen input value (when it exists) is the slope of the tangent line to the graph of the function at that point.
The process of finding a derivative is called differentiation. The reverse process of differentiation is called antidifferentiation. The fundamental theorem of calculus relates antidifferentiation with integration.
Differentiation and integration constitute the 2 fundamental operations in single-variable calculus.
Table of Contents
Common Function
The derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change of the variable x.
It is called “the derivative of f with respect to x”. If x and y are real numbers, and if the graph of f is plotted against x, the derivative is the slope of this graph at each point.
Review the differentiation rules for all the common function types.
| Function | Derivative | |
| Polynomials | 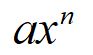 | |
| Radicals | ||
| Trigonometric functions | sin(x) | cos(x) |
| cos(x) | – Sin(x) | |
| tan(x) | ||
| cot(x) | ||
| sec(x) | ||
| csc(x) | ||
| Inverse trigonometric functions | ||
| Exponential functions | ||
| Logarithmic functions | ||
Examples
| Function | Application | Derivative | |
| Polynomials | |||
| Radicals | |||
| Trigonometric functions | sin(x) | cos(x) | cos(x) |
| cos(x) | – sin(x) | – sin(x) | |
| tan(x) | |||
| cot(x) | |||
| sec(x) | |||
| csc(x) | |||
| Inverse trigonometric functions | |||
| Exponential functions | |||
| Logarithmic functions | |||
Derivative rules
The derivative of a function can be computed from the definition by considering the difference quotient & computing its limit.
Once the derivatives of some simple functions are known, the derivatives of other functions are computed more easily using rules for obtaining derivatives of more complicated functions from simpler ones.
Here are simple rules to help you work out the derivatives of some functions.
| Rules | Function | Derivative |
| Multiplication by constant | cf | cf’ |
| Power Rule | xn | nxn-1 |
| Sum Rule | f + g | f’ + g’ |
| Difference Rule | f – g | f’ – g’ |
| Product Rule | f g | f g’ + f’ g |
| Quotient Rule | f/g | (f g’ – f’ g)/g2 |
| Chain Rule | f (g(x)) | f’(g(x)) g’(x) |
| Reciprocal Rule | 1/f | -f’/f2 |
Examples
| Rules | Function | Application | Derivative |
| Multiplication by constant | 7(2x3) | 7 × (2 × 3 × x3-1) | 42x2 |
| Power Rule | x7 | 7x7-1 | 7x6 |
| Sum Rule | x7 + x6 | 7x7-1 + 6x6-1 | 7x6 + 6x5 |
| Difference Rule | X5 – x6 | 5x5-1 – 6x6-1 | 5x4 + 6x5 |
| Product Rule | sin(x) cos(x) | sin(x)(-sin(x)) – cos(x)cos(x) | – sin2(x) + cos2(x) |
| Chain Rule | sin(x3) | cos(x3)×3x2 | 3x2cos(x3) |
| Reciprocal Rule | | |
