Bayes’ Theorem: Definition, Notation, Examples

Thomas Bayes named a theory about conditional probability. He was British mathematician in 18^th century. The theorem is Bayes’ Theorem.

Bayes’ theorem is used in statistics, medicine and pharmacology, finance, etc.

Definition of Bayes’ Theorem

Bayes’ theorem is a probability theorem when we have known another probability before. If the probability of blue ball outcomes is ¼ then Bayes’ theorem is used to determine the probability of red ball outcomes after the blue ones.

In another words, Bayes’ theorem is a way to predict existing probability after the previous condition.

Bayes’ theorem is also called as Bayes’ rule.

Bayes’ Theorem Notation

If there is two occurrences,

A : blue ball outcome

B : red ball outcome

Then probability of blue ball outcome happened given that red ball happened is

P(A|B) = {P(A) P(B|A)} / P(B)

It is called as Bayes’ Theorem

Where,

• P(A) : probability of blue ball outcome
• P(B) : probability of red ball outcome
• P(A|B) probability of blue ball outcome happens given that red ball outcome happens
• P(B|A) : probability of red ball outcome happens given that blue ball outcome happens

Based on general form of the Bayes’ theorem, there is also another form of Bayes’ theorem.

P(B) P(A|B) = P(A) P(B|A)

But, sometimes there are another form of Bayes’ Theorem.

P(B) can be describe to be longer form in some cases.

Based on the example, P(B) = {P(A) P(B|A) + P(~A) P(B|~A)}

Then the Bayes’ theorem

P(A|B) = {P(A) P(B|A)} / {P(A) P(B|A) + P(~A) P(B|~A)}

In another words,

Let A₁, A₂, A₃, … A_i are a set of events in space S, and they have non-zero occurrence probability. Let B be any event associated with S, then Bayes’ Theorem:

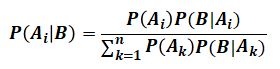
Another case that using longer form of P(B):

If there are two baskets of mangoes, A and B. It has been known percentage of ready to eat mangoes in each basket. A customer takes randomly a ready to eat mango and he take from first basket. The question is determining the probability.

The solution is:

• Making a notation to “taking a ready to eat mango, mangoes in first and second basket, and ready to eat mangoes in each basket”.
  M = taking a ready to eat mango
  A = mangoes in first basket → P(A)
  B = mangoes in second basket → P(B)
  P(M|A) = ready to eat mangoes in first basket
  P(M|B) = ready to eat mangoes in second basket

• Then the Bayes’ theorem is

P(A|M) = {P(A)P(M|A)} / {P(A)P(M|A) +P(B)P(M|B)}

Note: look at examples no.3 for complete case.

Bayes’ theorem Examples

1. In a class there are 50% of the boys like mathematics and 45% of the boys like physics.
Given that 20% of those that like mathematics and physics, what percent of those that like physics and mathematics?

2. In an office there are two favorite drink, they are coffee and tea. 65% of employees like tea and 30% of them like to drink coffee. But, 40% of them like coffee and tea. Determine percentage of employees that prefer to drink tea and coffee.

3. If there are two baskets of mangoes, A and B. 70% mangoes in basket A is ready to eat and 25% mangoes in basket B is not ready to eat yet. A customer takes randomly a ready to eat mango and he take from first basket. Determine the probability.

4. Arnold has two pockets. The first has 7 chocolate and 2 strawberry candies and the second has 5 chocolate and 9 strawberry candies. He takes a candy at random and it turns out to be chocolate. Determine the probability that the chocolate candy was from the first pocket.

5. In a restaurant there is a drug test for waiters dan chef that is 98% accurate, meaning 98% of the time it shows a true positive result for someone using the drug and 98% of the time it shows a true negative result for non-users of the drug.

Assume 0.8% of people use the drug. If a person selected at random tests positive for the drug, determine the probability the person is actually a user of the drug.