Table of Contents
Definition of Asymptote
Asymptote is a line or curve that approach to another curve. It can be horizontal, vertical, or oblique asymptote. Asymptote is always approach to the curve but the distance is never zero. In another words, asymptote is never same as the curve.
In mathematics, especially in analytic geometry, there are so many types of curve and the function. But, not all type has the asymptote. It is only rational function that has asymptote. Form of rational function is
f(x)/g(x)
Where f(x) and g(x) are polynomials and g(x) is not zero. The domain is all of real numbers except number that make g(x)=0.
Horizontal asymptote
Horizontal asymptote is parallel with x- axis. There are some rules about horizontal asymptote:
1. If the highest power of numerator and denominator are same, then the asymptote is coefficient of numerator over coefficient of denominator.
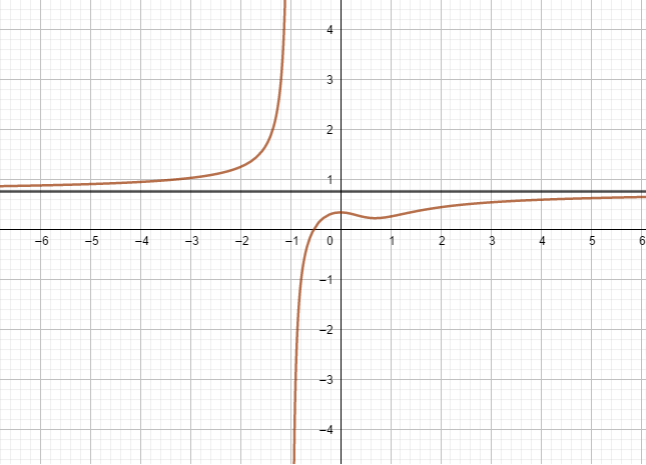
Example:
F(x) = (3x3-2x2+1)/(4x3+x2+3)
The asymptote is y=3/4
Look at the picture.
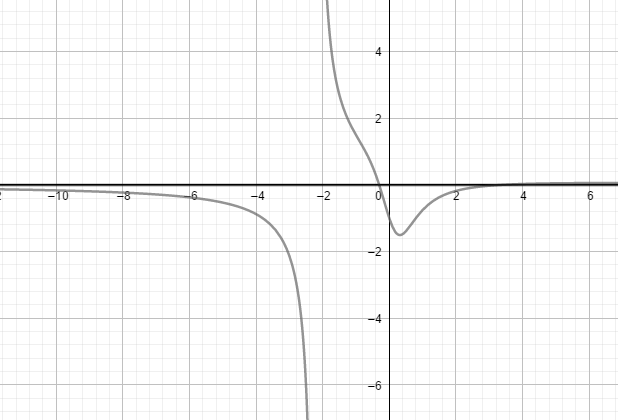
2. If the highest power of numerator is less than the highest power of denominator, then the asymptote is y=0
Example:
F(x) = (x2-3x-1)/(x3+2x2+1)
Asymptote is y=0
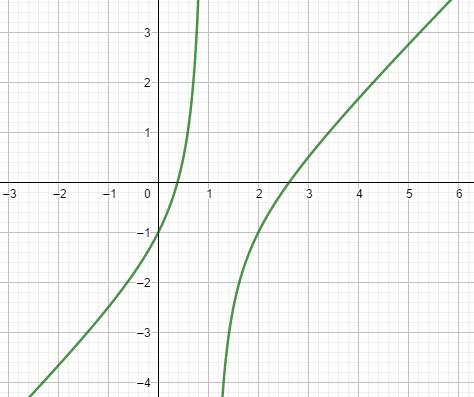
3. If the highest power of numerator is greater than the highest power of denominator, then there is no horizontal asymptote.
Example:
F(x) = (x2-3x+1)/(x-1)
There is no horizontal asymptote
Vertical asymptote
Vertical asymptote is parallel with y- axis. There is no horizontal and vertical asymptote in a curve. For example, take the third rules in horizontal asymptote.
There is no horizontal asymptote if the highest power of numerator is greater than the highest power of denominator.
Take the example:
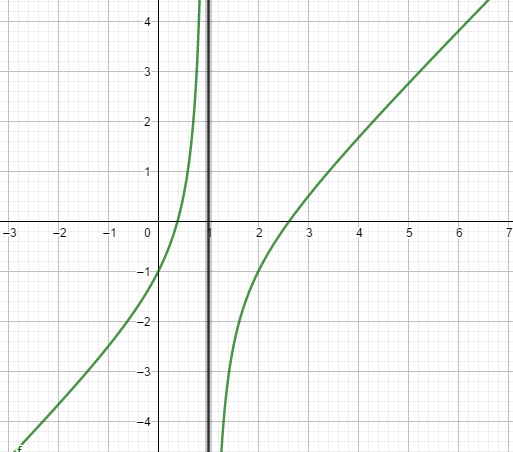
F(x) = (x2-3x+1)/(x-1)
= (x-2) –(1/(x-1))
It means the result is x-2 and the remainder is -1/(x-1).
If the value of x gets closer and closer to infinite, then -1/(x-1) get closer to zero.
The vertical asymptote is x=1. It is because x=1 make the remainder to be zero.
Look at the picture of vertical asymptote
Oblique asymptote
Oblique asymptote is asymptote that is not parallel neither with x-axis nor y-axis.
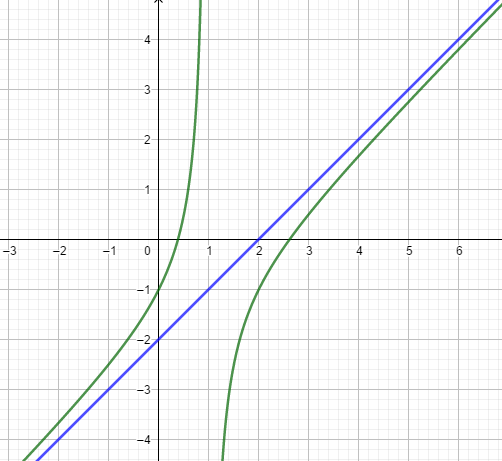
Take the example from the third rule of horizontal asymptote:
F(x) = (x2-3x+1)/(x-1)
= (x-2) –(1/(x-1))
It means the result is x-2 and the remainder is -1/(x-1).
Consequently, the oblique asymptote is x-2.
In another words, based on the problem, there are rules about oblique asymptote:
- Oblique asymptote exists if the greater power of numerator is one more than the greater power of denominator.
- Numerator can’t be divided by the denominator.
Look at the picture of oblique asymptote
Examples of Asymptote’s Problem
1. Define which one the most possibly function based on the picture below!
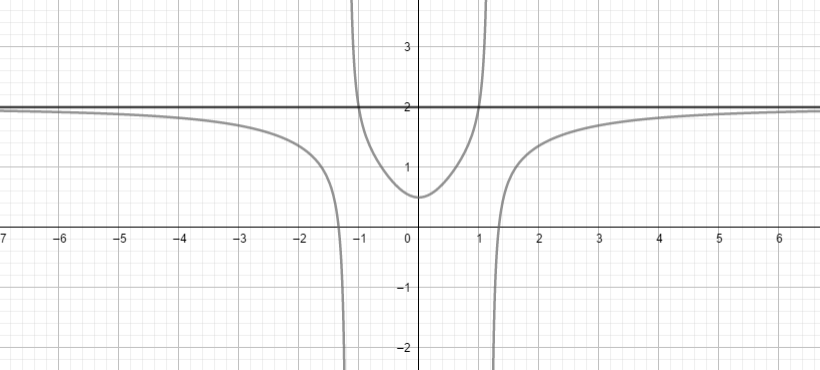
a. F(x) = (2x4-3x2-1)/(x4-2)
b. F(x) = (3x5-2x3-2)/(3x3-2)
c. F(x) = (2x3-5x-2)/(4x5-2x4+8)
d. F(x) = (x-2)/3
e. F(x) = 2
Based on the picture, the most possibly answer is (a) F(x) = (2x4-3x2-1)/(x4-2). It is because the asymptote on the picture is on y=2.
Based on the rules of horizontal asymptote, if the highest power of numerator and denominator are same, then the asymptote is coefficient of numerator over coefficient of denominator.
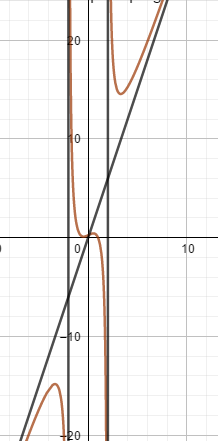
2. Given function f(x) = (3x3-2x-1)/(x2-4), determine the vertical asymptote and how the graph!
Function f(x) = (3x3-2x-1)/(x2-4), because of the power of numerator is greater than denominator, calculate it first. The result is 3x and the remainder is (10x-1)/(x2-4).
There are vertical asymptote x=2 and x=-2, and oblique asymptote y=3x.